
【题目】已知:在四边形ABCD中,E、F、G、H分别是BC、AD、BD、AC的中点.
①求证:EF与GH互相平分;
②当四边形ABCD的边满足______ 条件时,EF⊥GH.并说明理由.

【答案】AB=CD
【解析】
试题(1)连接GE、GF、HF、EH,根据三角形的中位线定理即可证得EG=FH/GF=EH,则四边形EHFG是平行四边形,
利用平行四边形的性质即可证得;
(2)EF⊥GH时能得到四边形EHFG四边相等,从而得到四边形ABCD的四边相等.
试题解析:
(1)连接GE、GF、HF、EH.
∵E、G分别是AD、BD的中点,
∴EG=![]() CD,
CD,
同理FH=![]() CD,FG=
CD,FG=![]() AB,EH=
AB,EH=![]() AB
AB
∴EG=FH、GF=EH
∴四边形EHFG是平行四边形.
∴EF与GH互相平分;
(2)当EF⊥GH时,四边形EHFG是菱形,
此时GF=FH=HE=EG,
∵EG=![]()
CD,FH=![]() CD,FG=
CD,FG=![]() AB,EH=
AB,EH=![]() AB
AB
∴AB=BC=CD=DA,
∴当四边形ABCD的边满足条件AB=BC=CD=DA时,EF⊥GH.


科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠BAC=90°,过点C的直线EF∥AB,D是BC上一点,连接AD,过点D分别作GD⊥AD,HD⊥BC,交EF和AC于点G,H,连接AG.
(1)当∠ACB=30°时,如图1所示.
①求证:△GCD∽△AHD;
②试判断AD与DG之间的数量关系,并说明理由;
(2)当tan∠ACB= ![]() 时,如图2所示,请你直接写出AD与DG之间的数量关系.
时,如图2所示,请你直接写出AD与DG之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证: 
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
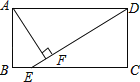
A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计, ![]() ≈1.7,结果精确到1m,则该楼的高度CD为( )
≈1.7,结果精确到1m,则该楼的高度CD为( ) 
A.47m
B.51m
C.53m
D.54m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴相交的于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
(1)直接写出A,B,C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点(P不与C,B两点重合),过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形.
②设△BCF的面积为S,求S与m的函数关系式;当m为何值时,S有最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com