
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感.他惊喜的发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程:
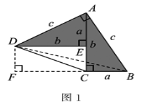
(1)将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°.求证:a2+b2=c2.
(2)请参照上述证法,利用图2完成下面的证明.
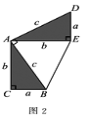
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.
求证:a2+b2=c2.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
证明勾股定理时,用几个全等的直角三角形拼成一个规则的图形,然后利用大图形的面积等于几个小图形的面积和,化简整理即可得到勾股定理表达式.具体:(1) 连接DB,过点D作BC边上的高DF,则DF=EC=b-a,表示出S四边形ADCB, 两者相等,整理即可得证; (2)证法(一) 首先连结BD,过点B作DE边上的高BF,则BF=b-a,表示出S五边形ACBED,两者相等,整理即可得证; 证法二:连接BD,过点B作DE边上的高BF,则BF=b-a,表示出S五边形ACBED,两者相等,整理即可得证.
(1)证明:连接DB,过点D作BC边上的高DF,则DF=EC=b-a.
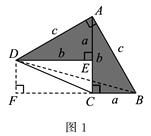
∵S四边形ADCB=S△ACD+S△ABC=![]() b2+
b2+![]() ab,
ab,
又∵S四边形ADCB=S△ADB+S△DCB=![]() c2+
c2+![]() a(b-a),
a(b-a),
∴![]() b2+
b2+![]() ab=
ab=![]() c2+
c2+![]() a(b-a).
a(b-a).
∴a2+b2=c2.
(2)证法一:连接BD,过点B作DE边上的高BF,则BF=b-a.
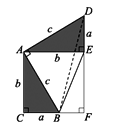
∵S五边形ACBED=S△ACB+S△ABE+S△AED=![]() ab+
ab+![]() b2+
b2+![]() ab,
ab,
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=![]() ab+
ab+![]() c2+
c2+![]() a(b-a),
a(b-a),
∴![]() ab+
ab+![]() b2+
b2+![]() ab=
ab=![]() ab+
ab+![]() c2+
c2+![]() a(b-a),
a(b-a),
∴a2+b2=c2.
证法二:连接BD,过点B作DE边上的高BF,则BF=b-a,
∵S五边形ACBED=S梯形ACBE+S△AED=![]() b(a+b)+
b(a+b)+![]() ab,
ab,
又∵S五边形ACBED=S△ACB+S△ABD+S△BED=![]() ab+
ab+![]() c2+
c2+![]() a(b-a),
a(b-a),
∴![]() b(a+b)+
b(a+b)+![]() ab=
ab=![]() ab+
ab+![]() c2+
c2+![]() a(b-a),
a(b-a),
∴a2+b2=c2.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求直线AB和OB的解析式.
(2)求抛物线的解析式.
(3)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.问△BOD的面积是否存在最大值?若存在,求出这个最大值并写出此时点D的坐标;若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高速公路的同一侧有A、B两城镇,如图,它们到高速公路所在直线MN的距离分别为AA′=2 km,BB′=4 km,A′B′=8 km.要在高速公路上A′、B′之间建一个出口P,使A、B两城镇到P的距离之和最小.求这个最短距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D,E,F是垂足,且AB=5,BC=4,AC=3,则点O到三边AB,AC,BC的距离分别是( )
A. 1,1,1 B. 2,2,2 C. 1,1.5,2 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二年级教师对试卷讲评课中学生参与情况进行调查,调查项目分为主动质疑、独立思考、专注听讲、讲解题目四项.调查组随机抽取了若干名初中学生的参与情况,绘制了如图所示的扇形统计图和条形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为______度;
(2)请将频数分布直方图补充完整;
(3)如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明 : ∠ABC=∠BFD ;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形AOCD的边OC在x轴上,O为坐标原点,CD垂直于x轴,D(5,4),AD=2.若动点E、F同时从点O出发,E点沿折线OA→AD→DC运动,到达C点时停止;F点沿OC运动,到达C点时停止,它们运动的速度都是每秒1个单位长度.设E运动x秒时,△EOF的面积为y(平方单位),则y关于x的函数图象大致为( )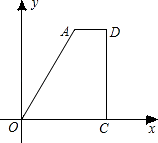
A.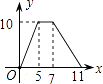
B.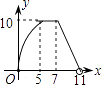
C.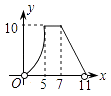
D.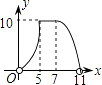
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com