
在Rt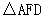 中,∠F=90°,点B、C分别在AD、FD上,以AB为直径的半圆O
过点C,
中,∠F=90°,点B、C分别在AD、FD上,以AB为直径的半圆O
过点C,
联结AC,将△AFC 沿AC翻折得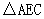 ,且点E恰好落在直径AB上.
,且点E恰好落在直径AB上.
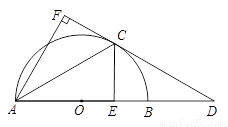
(1)判断:直线FC与半圆O的位置关系是_______________;并证明你的结论.
(2)若OB=BD=2,求CE的长.
科目:初中数学 来源: 题型:
在Rt![]() 中,∠F=90°,点B、C分别在AD、FD上,以AB为直径的半圆O过点C,
中,∠F=90°,点B、C分别在AD、FD上,以AB为直径的半圆O过点C,
联结AC,将△AFC 沿AC翻折得![]() ,且点E恰好落在直径AB上.
,且点E恰好落在直径AB上.
(1)判断:直线FC与半圆O的位置关系是_______________;并证明你的结论.
(2)若OB=BD=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源:2013届江苏省无锡市新区第一实验学校九年级下学期期中考试数学试卷(带解析) 题型:填空题
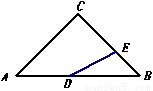
如图,在Rt 中,∠C=90°,∠ABC=45°,AB=6,点D在AB边上,点E在BC边上(不与点B、C重合),且DA=DE,则AD的取值范围是 .
中,∠C=90°,∠ABC=45°,AB=6,点D在AB边上,点E在BC边上(不与点B、C重合),且DA=DE,则AD的取值范围是 . 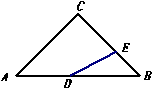
查看答案和解析>>
科目:初中数学 来源:2011届北京市丰台区5月中考数学一模试卷 题型:解答题
在Rt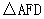 中,∠F="90°,点B、C分别在AD、FD上,以AB为直径的半圆O" 过点C,
中,∠F="90°,点B、C分别在AD、FD上,以AB为直径的半圆O" 过点C,
联结AC,将△AFC 沿AC翻折得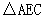 ,
, 且点E恰好落在直径AB上.
且点E恰好落在直径AB上.
(1)判断:直线FC与半圆O的位置关系是________ _____
_____ __;并证明你的结论.
__;并证明你的结论.
(2)若OB="BD=2,求CE的长." 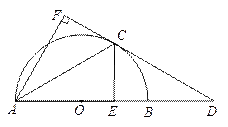
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省无锡市新区第一实验学校九年级下学期期中考试数学试卷(解析版) 题型:填空题
如图,在Rt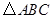 中,∠C=90°,∠ABC=45°,AB=6,点D在AB边上,点E在BC边上(不与点B、C重合),且DA=DE,则AD的取值范围是 .
中,∠C=90°,∠ABC=45°,AB=6,点D在AB边上,点E在BC边上(不与点B、C重合),且DA=DE,则AD的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com