练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．先化简，再求值：[（a-b）2+（2a+b）（1-b）-b]÷（-$\frac{1}{2}$a），其中a、b满足|a+1|+（2b-1）2=0．

    分析 根据完全平方公式以及多项式乘多项式的法则化简展开，再根据非负数的性质求出a、b代入即可．

    解答 解：原式=（a2-2ab+b2+2a-2ab+b-b2-b）÷（-$\frac{1}{2}$a），
    =（a2-4ab+2a）÷（-$\frac{1}{2}$a），
    =-2a+8b-4，
    ∵|a+1|+（2b-1）2=0，
    又∵|a+1|≥0，（2b-1）2≥0，
    ∴a=-1．b=$\frac{1}{2}$，
    ∴原式=2+4-4=2．

    点评 本题考查整式的混合运算，乘法公式，多项式乘多项式法则等整式，解题的关键是灵活运用这些知识解决问题，注意符号问题，属于中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    2．分解因式：2a-a2=a（2-a）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．求代数式$\frac{{{x^2}-x}}{{{x^2}-2x+1}}÷（\frac{1}{x-1}-1）$的值，其中$x=2-\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．化简：$\frac{x+3}{{x}^{2}-9}$+$\frac{1}{x-3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．先化简再求值：（$\frac{{x}^{2}}{x-1}$-4）÷（x+1）•$\frac{{x}^{2}-1}{{x}^{2}-2x}$，其中x=$\sqrt{2}$+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．某校举办初中生演讲比赛，每班派一名学生参赛，现某班有A，B，C三名学生竞选，他们的笔试成绩和口试成绩分别用两种方式进行了统计，如表和图1：
    学生ABC
    笔试成绩（单位：分）859590
    口试成绩（单位：分）908085

    （1）请将表和图1中的空缺部分补充完整．
    （2）竞选的最后一个程序是由本年级段的300名学生代表进行投票，每票计1分，三名候选人的得票情况如图2（没有弃权票，每名学生只能推荐一人），若将笔试、口试、得票三项测试得分按3：4：3的比例确定最后成绩，请计算这三名学生的最后成绩，并根据最后成绩判断谁能当选．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

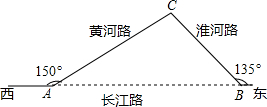    3．如图，已知：长江路西段与黄河路的夹角为150°，长江路东段与淮河路的夹角为135°，黄河路全长AC=20km，从A地道B地必须先走黄河路经C点后再走淮河路才能到达，城市道路改造后，直接打通长江路（即修建AB路段）．问：打通长江路后从A地道B地可少走多少路程？（参考数据：$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．反比例函数y=$\frac{k}{2x}$（k为非零常数）的图象在其所在象限内，y的值随x值的增大而增大，那么函数y=$\frac{2}{k}$x的图象经过第（　　）象限．
    A．一、二B．一、三C．二、三D．二、四

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列命题是假命题的是（　　）
    A．两个角的和等于平角时，这两个角互为补角
    B．平行于同一直线的两直线平行
    C．垂直于同一直线的两直线平行
    D．如果$\frac{a}{c}$=$\frac{b}{c}$那么a=b

    查看答案和解析>>

    同步练习册答案