
如图(1),∆ABC为等边三角形,AB=6,在直角三角板DEF中∠F=90°,∠FDE=60°,点D在边BC上运动,边DF始终经过点A,DE交AC于点G.
(1)求证:①∠BAD=∠CDG
②∆ABD∽∆DCG
(2)设BD=x,若CG= ,求x的值;
,求x的值;
(3)如图2,当D运动到BC中点时,点P为线段AD上一动点,连接CP,将线段CP绕着点C逆时针旋转60°得到CP' ,连接BP',DP',
①求∠CBP'的度数;②求DP'的最小值.
(1)①详见解析;②详见解析;(2)x1=1,x2=5;(3) ①∠CBP'="30°" ; ②DP′=1.5.
解析试题分析:(1) ①利用三角形的一个外角等于和它不相邻的两个内角的和,即可求证. ②利用两角相等的三角形相似.(2)利用前面所得的三角形相似,由对应边成比例,可求得x的值.(3)①根据旋转的性质,旋转前后的图形对应线段、对应角相等,可证得△ACP≌△BCP′,从而∠CAP=∠CBP′,然后根据等腰三角形的“三线合一”性质,得到∠CBP′=30°. ②根据“垂线段最短”这一定理,当∠BP′D=90°时,DP′最短.
试题解析:(1)①∵∠ADC=∠B+∠BAD, ∠ADC=∠ADG+∠CDG
∴∠B+∠BAD=∠ADG+∠CDG
∵三角形ABC是等边三角形
∴∠B=∠C=60°
∵∠ADG=60°
∴∠BAD=∠CDG
②由①知∠BAD=∠CDG
∵∠B=∠C
∴△ABD∽△DCG
(2)由(1)知△ABD∽△DCG,所以AB:CD=BD:CG,CD=6-x,AB=6,CG= ,BD=x,代入可求得:x=1或5.
,BD=x,代入可求得:x=1或5.
(3) ①由旋转知∠PCP′=60°,CP=CP′,
∵△ABC是等边三角形
∴AC="BC," ∠ACB=60°
∴∠ACP=∠BCP′
∴△ACP≌△BCP′
∠CBP′=∠CAD=30°
②根据“垂线段最短”可知,当DP′⊥BP′时,DP′最短,此时,由于∠CBP′=30°,所以DP′= BD=1.5.
BD=1.5.
考点:1、相似三角形的判定和性质;2、旋转的性质;3、全等三角形的判定和性质


科目:初中数学 来源: 题型:解答题
如图①,已知线段AB=8,以AB为直径作半圆O,再以OA为直径作半圆C,P是半圆C上的一个动点(P与点A,O不重合),AP的延长线交半圆O于点D。
(1)判断线段AP与PD的大小关系,并说明理由;
(2)连接PC,当∠ACP=600时,求弧AD的长;
(3)过点D作DE⊥AB,垂足为E(如图②),设AP=x,OE=y,求y与x之间的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC.
求证:(1)点F是DC上一点,连接EF,交AC于点O(如图1),△AOE∽△COF;
(2)若点F是DC的中点,连接BD,交AE与点G(如图2),求证:四边形EFDG是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,在正方形ABCD中,AB=1,点E在AB延长线上,联结CE、DE,DE交边BC于点F,设BE ,CF
,CF .
.
图1
(1)求 关于
关于 的函数解析式,并写出
的函数解析式,并写出 的取值范围;
的取值范围;
(2)如图2,对角线AC、BD的交点记作O,直线OF交线段CE于点G,求证: ;
;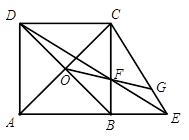
图2
(3)在(2)的条件下,当 时,求
时,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,∴P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.
(1)求证:△APB≌△APD;
(2)已知DF:FA=1:2,设线段DP的长为x,线段PF的长为y.
①求y与x的函数关系式;
②当x=6时,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形ABCD中,AB=12cm,AD=16cm,动点E、F分别从A点、C点同时出发,均以2cm/s的速度分别沿AD向D点和沿CB向B点运动。
(1)经过几秒首次可使EF⊥AC?
(2)若EF⊥AC,在线段AC上,是否存在一点P,使 ?若存在,请说明P点的位置,并予以证明;若不存在,请说明理由。
?若存在,请说明P点的位置,并予以证明;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com