
【题目】已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.

【答案】(1)115°;(2)证明见解析;(3)结论:当∠O=36°或90°时,CA分∠OCD成1:2两部分.
【解析】(1)根据平行线的性质可得∠O=∠MCB,由平角定义可得∠ACM=130°,再利用角平分线的定义可求∠DCM=65°,从而可求出∠BCD的度数;
(2)利用等角的余角相等证明∠ACE=∠ECO即可;
(3)结合(2)的结论可知∠BOC=∠BOM=∠DOM,从而得出结论.
解:(1)∵AB∥ON,
∴∠O=∠MCB(两直线平行,同位角相等).
∵∠O=50°,
∴∠MCB=50°.
∵∠ACM+∠MCB=180°(平角定义),
∴∠ACM=180°-50°=130°.
又∵CD平分∠ACM,
∴∠DCM=65°(角平分线定义),
∴∠BCD=∠DCM+∠MCB=65°+50°=115°,
(2)∵CE⊥CD,
∴∠DCE=90°,
∴∠ACE+∠DCA=90°..
又∵∠MCO=180°(平角定义),
∴∠ECO+∠DCM=90°,
∵∠DCA =∠DCM,
∴∠ACE=∠ECO(等角的余角相等),
即CE平分∠OCA;
(3)①当∠OCA: ∠ACD=1:2时,
设∠OCD=x°, ∠ACD=2x°,由题意得
x+2x+2x=180,
∴x=36,
∴∠O=∠OCA=x=36°;
②当∠ACD:∠OCA =1:2时,
设∠ACD =x°, ∠OCA =2x°,由题意得
x+x+2x=180,
∴x=45,
∴∠O=∠OCA=2x=2×45°=90°;
∴当∠O=36°或90°时,CA分∠OCD成1:2两部分.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】地球距离月球表面约为383900千米,那么这个数据用科学记数法表示为( )
A.3.839×104
B.3.839×105
C.3.839×106
D.38.39×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知∠B和∠C的平分线相交于点F,经过点F作DE∥BC,交AB于D,交AC于点E,若BD+CE=9,则线段DE的长为( ) 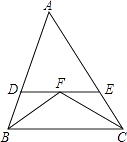
A.9
B.8
C.7
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A所表示的实数为5,点B所表示的实数为a,⊙A的半径为3,要使点B在⊙A内时,实数a的取值范围是( )
A.a>2B.a>8C.2<a<8D.a<2或a>8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
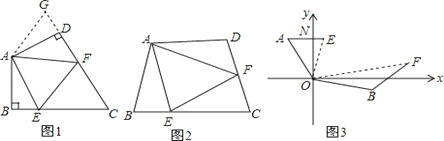
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD上述结论是否仍然成立,并说明理由;
∠BAD上述结论是否仍然成立,并说明理由;
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com