
����Ŀ��ij��ѧ������Ȥ�С����Χ��һ�����λ���������һ�߿�ǽ�����������ܳ�Ϊ![]() �����Χ�ɣ���֪ǽ��Ϊ
�����Χ�ɣ���֪ǽ��Ϊ![]() �ף���ͼ��ʾ���������������ֱ��ǽ��һ�߳�Ϊ
�ף���ͼ��ʾ���������������ֱ��ǽ��һ�߳�Ϊ![]() �ף�
�ף�

![]() �����������Ϊ
�����������Ϊ![]() ƽ���ף���
ƽ���ף���![]() ��
��
![]() ��ƽ����ǽ��һ�߳���С��
��ƽ����ǽ��һ�߳���С��![]() �ף������������������ֵ����Сֵ������У�������ֵ����Сֵ�����û�У���˵�����ɣ�
�ף������������������ֵ����Сֵ������У�������ֵ����Сֵ�����û�У���˵�����ɣ�
![]() ������������������
����������������С��![]() ƽ����ʱ��ֱ��д��
ƽ����ʱ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡�(1)x=10;(2) ��![]() ʱ��
ʱ��![]() ;(3)
;(3)![]()
��������
��1����������÷�����⼴�ɣ�
��2�������������Ϊy����������õ����κ�������ʽy=x��30-2x��=-2x2+30x�����ݶ��κ�����������⼴�ɣ�
��3��������ò���ʽ�����ɵõ����ۣ�
![]() ��������֪ƽ����ǽ��һ�ߵij�Ϊ
��������֪ƽ����ǽ��һ�ߵij�Ϊ![]() �ף�
�ף�
����![]() ��
��
��ã�![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
![]() �����������Ϊ
�����������Ϊ![]() ��
��
��![]() ��
��
��![]() ��
��
�����������![]() �����ֵ��
�����ֵ��
��![]() ��
��
��ã�![]() ��
��
��![]() ��
��
�൱![]() ʱ����ƽ����ǽ��һ�߳�
ʱ����ƽ����ǽ��һ�߳�![]() �ף�
�ף�![]() ƽ���ף�
ƽ���ף�
��![]() ʱ��
ʱ��![]() ��
��
![]() �������
�������![]() ��
��
��ã�![]() ��
��![]() ��
��
�֡�![]() ��
��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��![]() +
+![]() +2��x���ཻ��A��B���㣬����A��B����ࣩ��y�ύ�ڵ�C��
+2��x���ཻ��A��B���㣬����A��B����ࣩ��y�ύ�ڵ�C��
��1����A��B�������꣮
��2������AC������P�ڵ�һ�����������ϣ�P�ĺ�����Ϊt���ı���ABPC�����ΪS�����ú�t��ʽ�ӱ�ʾS������tΪ��ֵʱ��S���

��3���ڣ�2���Ļ����ϣ��������������ϺͶԳ������Ƿ�ֱ���ڵ�G�͵�H��ʹ��A��G��H��P�ĵ㹹�ɵ��ı���Ϊƽ���ı��Σ������ڣ���ֱ��д��G��H�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��2019��11��21��---11��27�������������ͼ��������˵������ȷ���ǣ� ��

A.21��---22�յ�������³���������
B.��7���У�23�յ�������¸�������6��ĵ��������
C.23---25�յ�������³��½�����
D.���������У�24��---25�յ�������±仯���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABC�У�AB=AC��D��E�ֱ���AB��AC�ϣ�AD=AE������ADE�Ƶ�A��ʱ��������ת.

��1�����֣���ͼ2������BD��CE������BAC=60����D��ǡ���߶�BE�ϣ����BEC= ����
��2��̽������ͼ3������BD��CE�������ڵ�F����֤����BFC=��BAC��
��3����չ����ͼ4������BAC=90����AB=5��AD=2������CD��BE����ֱ��д���ı���BCDE��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڿ�20�ף���32�ľ��θ����ϣ�����ͬ����������·(��������һ�������Һ����������ഹֱ)���������طֳɴ�С��ȵ����������Ҫʹ������������570ƽ���ף��ʵ�·Ӧ�ö��?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
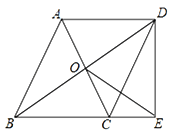
����Ŀ����ͼ����ABCD�ĶԽ��߽��ڵ�O����E�ڱ�BC���ӳ����ϣ���OE=OB������DE��
��1����֤����BDE��ֱ�������Σ�
��2�����OE��CD�����ж���BDE����DCE�Ƿ����ƣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=kx2+2kx��3k��k��0������ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����OC=OA��
��1����A����Ϊ�� ������B����Ϊ�� ���������ߵĽ���ʽΪ�� ����
��2������P�ǵڶ��������������ϵ�һ�����㣬����AP��CP�����ı���ABCP��������ʱ�����P�����ꣻ
��3������Q��0��m����y���ϵĶ��㣬����AQ��BQ��
������AQB�Ƕ۽�ʱ����m��ȡֵ��Χ��
������AQB=60��ʱ����m=�� ������ֱ��д���𰸣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ι��ţ���������ˮ��2mʱ��ˮ���4m����ˮ���½�1mʱ��ˮ���������_____m��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com