
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度向终点
出发,以每秒3个单位长度的速度向终点![]() 运动,过点
运动,过点![]() 作
作![]() 交
交![]() 边或
边或![]() 边于点
边于点![]() ,点
,点![]() 是射线
是射线![]() 边上一点,总保持
边上一点,总保持![]() ,以
,以![]() 、
、![]() 为邻边构造矩形
为邻边构造矩形![]() ,设矩形
,设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() .
.
(1)用含![]() 的式子表示线段
的式子表示线段![]() 的长;
的长;
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值;
的值;
(3)当矩形![]() 与
与![]() 重叠部分图形为四边形时,求
重叠部分图形为四边形时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)点![]() 与点
与点![]() 同时出发,在线段
同时出发,在线段![]() 上以每秒5个单位长度的速度沿
上以每秒5个单位长度的速度沿![]() 往返一次,连结
往返一次,连结![]() 、
、![]() ,直接写出矩形
,直接写出矩形![]() 的面积是
的面积是![]() 的面积的2倍时
的面积的2倍时![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(4)
;(4)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)由题意可知:![]() ,PB=3t,据此解答即可;
,PB=3t,据此解答即可;
(2)先根据勾股定理求出AC的长,当点![]() 落在
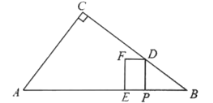
落在![]() 上时,如图1,在Rt△DPB中先利用∠A的正切用含t的代数式表示出DP,即为EF,再在Rt△AEF中利用三角函数的知识用含t的关系式表示出AE,由AE+EP+PB=5可得关于t的方程,解方程即得结果;
上时,如图1,在Rt△DPB中先利用∠A的正切用含t的代数式表示出DP,即为EF,再在Rt△AEF中利用三角函数的知识用含t的关系式表示出AE,由AE+EP+PB=5可得关于t的方程,解方程即得结果;
(3)当![]() 时,根据(2)题的结果利用三角形的面积公式直接解答即可;当C、D重合时,如图2,当A、E两点重合时,如图3,分别求出这两种情况t的值,进而可得矩形
时,根据(2)题的结果利用三角形的面积公式直接解答即可;当C、D重合时,如图2,当A、E两点重合时,如图3,分别求出这两种情况t的值,进而可得矩形![]() 与
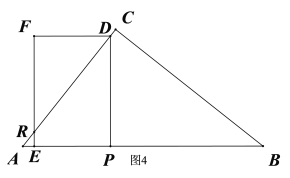
与![]() 重叠部分图形为四边形时t的范围,再结合图4利用三角函数的知识用含t的代数式表示出DP和RE,然后根据梯形的面积公式解答即可;
重叠部分图形为四边形时t的范围,再结合图4利用三角函数的知识用含t的代数式表示出DP和RE,然后根据梯形的面积公式解答即可;
(4)分H、D重合之前,如图5;H、D重合以后,D、H仍在BC边上,如图6;点D在AC边上、点H在BC边上,如图7共三种情况,先利用三角函数的知识用含t的代数式表示出DP边上的高HT的长,再根据矩形![]() 的面积是
的面积是![]() 的面积的2倍即可列出关于t的方程,解方程即可求得结果.
的面积的2倍即可列出关于t的方程,解方程即可求得结果.
解:(1)∵![]() ,PB=3t,
,PB=3t,
∴![]() ;
;
(2)在![]() 中,∵
中,∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
当点![]() 落在
落在![]() 边上时,如图1,在Rt△DPB中,
边上时,如图1,在Rt△DPB中,![]() ,
,
∵四边形![]() 是矩形,∴EF=DP
是矩形,∴EF=DP![]() ,
,
在Rt△AEF中,![]() ,
,
∵AE+EP+PB=5,
∴![]() ,解得:
,解得:![]() ;
;
(3)当![]() 时,重合部分为四边形,由(2)题知:
时,重合部分为四边形,由(2)题知:![]() ;
;
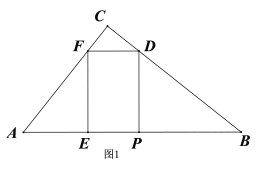
当C、D重合时,如图2,此时重合部分为四边形,![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
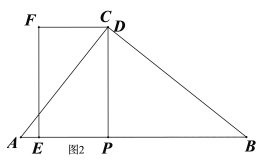
当A、E两点重合时,如图3,此时重合部分为三角形,AP=![]() ,由AP+BP=5,得
,由AP+BP=5,得![]() ,解得:
,解得:![]() ,
,
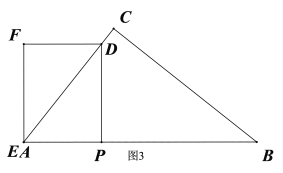
∴当![]() 时,如图4,
时,如图4,![]() ,
,
∴![]() ;
;
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;
;
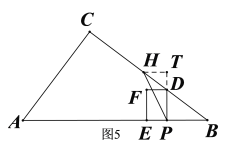
(4)①当H、D重合之前,由题意知CH=5t,![]() ,∴
,∴![]() ,
,
于是当![]() 时,过点H作HT⊥PD交PD延长线于点T,如图5,则
时,过点H作HT⊥PD交PD延长线于点T,如图5,则![]() ,
,
若矩形![]() 的面积是
的面积是![]() 的面积的2倍,则
的面积的2倍,则![]() ,
,
解得:![]() ,或t=0(舍去);
,或t=0(舍去);
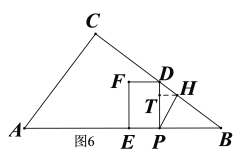
②当H、D重合以后,D、H仍在BC边上,如图6,此时![]() ,
,![]() ,
,
若矩形![]() 的面积是
的面积是![]() 的面积的2倍,则
的面积的2倍,则![]() ,
,
解得:![]() ,或t=0(舍去);
,或t=0(舍去);
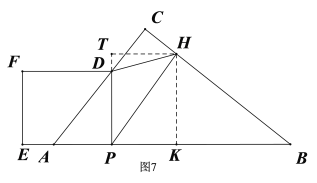
③当点D在AC边上、点H在BC边上时,即![]() ,如图7,作HK⊥AB于点K,则
,如图7,作HK⊥AB于点K,则![]() ,
,![]() ,
,
若矩形![]() 的面积是
的面积是![]() 的面积的2倍,则
的面积的2倍,则![]() ,
,
即![]() ,解得:
,解得:![]() .
.
综上所述:若矩形![]() 的面积是
的面积是![]() 的面积的2倍,t=
的面积的2倍,t=![]() 或
或![]() 或
或![]() .
.


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每盒150元,每台新机最多可配买24盒;若非同时配买,则每盒需220元.
公司根据以往的记录,十台打印机正常工作五年消耗墨盒数如表:
消耗墨盒数 | 22 | 23 | 24 | 25 |
打印机台数 | 1 | 4 | 4 | 1 |
(1)以这十台打印机消耗墨盒数为样本,估计“一年该款打印机正常工作5年消耗的墨盒数不大于24”的概率;
(2)试以这10台打印机5年消耗的墨盒数的平均数作为决策依据,说明购买10台该款打印机时,每台应统一配买23盒墨还是24盒墨更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
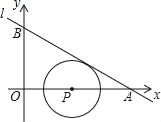
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
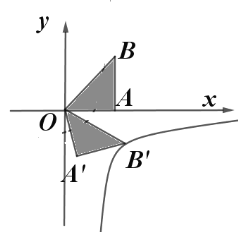
【题目】如图,等腰直角三角形![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,将
,将![]() 绕顶点
绕顶点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,使点
,使点![]() 落在双曲线
落在双曲线![]() 的图象上,则
的图象上,则![]() ________,该双曲线的函数解析式为________.
________,该双曲线的函数解析式为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
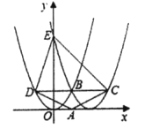
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 的图像交于点
的图像交于点![]() ,抛物线
,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交两抛物线于
轴的平行线交两抛物线于![]() 、
、![]() 两点.若点
两点.若点![]() 是
是![]() 轴上两抛物线顶点之间的一点,连结
轴上两抛物线顶点之间的一点,连结![]() ,
,![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为________(用含
的面积为________(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
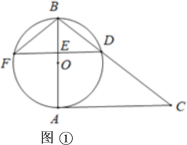
【题目】已知AB是⊙O的直径,AC是⊙O的切线,∠ABC=52°,BC交⊙O于点D,E是AB上一点,延长DE交⊙O于点F.
(Ⅰ)如图①,连接BF,求∠C和∠DFB的大小;
(Ⅱ)如图②,当DB=DE时,求∠OFD的大小.
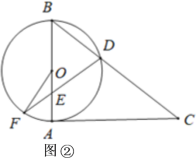
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式变得更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息回答下列问题:

(1)本次调查共调查了______名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为______;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级数学兴趣小组在研究等腰直角三角形与图形变换时,作了如下研究:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为腰作等腰直角三角形DAF,使∠DAF=90°,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①CF与BC的位置关系为 ;
②CF,DC,BC之间的数量关系为 (直接写出结论);
(2)数学思考
如图2,当点D在线段CB的延长线上时,(1)中的①、②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,将△DAF沿线段DF翻折,使点A与点E重合,连接CE,若已知4CD=BC,AC=2![]() ,请求出线段CE的长.
,请求出线段CE的长.
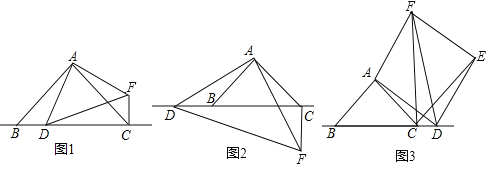
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,AC长为![]() ,若将边AC平移至A'C'处,此时A'坐标为(-4,2),分别连接A'B,C'O,反比例函数y=
,若将边AC平移至A'C'处,此时A'坐标为(-4,2),分别连接A'B,C'O,反比例函数y=![]() 的图象与四边形A'BOC'对角线A'O交于D点,连接BD,则当BD取得最小值时,k的值是______ .
的图象与四边形A'BOC'对角线A'O交于D点,连接BD,则当BD取得最小值时,k的值是______ .
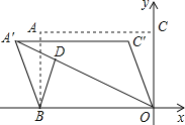
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com