
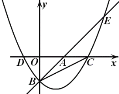
【题目】如图,直线y=x-3与坐标轴交于A、B两点,抛物线![]() 经过点B,与直线y=x-3交于点E(8,5),且与x轴交于C,D两点.
经过点B,与直线y=x-3交于点E(8,5),且与x轴交于C,D两点.
(1)求抛物线的解析式;
(2)抛物线上有一点M,当∠MBE=75°时,求点M的横坐标;
(3)点P在抛物线上,在坐标平面内是否存在点Q,使得以点P,Q,B,C为顶点的四边形是矩形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在矩形,
;(3)存在矩形,![]()
【解析】
(1)直线y=x-3与坐标轴交于A、B两点,则A(3,0)B(0,-3),把B、E点坐标代入二次函数方程,解得:抛物线的解析式y=![]() x2-x-3…①;
x2-x-3…①;
(2)当∠MBE=75°时,如下图所示,分M在x轴上和x轴下分别求解即可;
(3)存在①当BC为矩形对角线时,矩形BP′CQ′所在的位置如图所示,设:P′(m,n),n=-![]() m2-m-3…③,
m2-m-3…③,
P′C所在直线的k1=![]() ,P′B所在的直线k2=
,P′B所在的直线k2=![]() ,则:k1k2=-1即可求解,②当BC为矩形一边时,矩形BCQP所在的位置如图所示,直线BC所在的方程为:y=-
,则:k1k2=-1即可求解,②当BC为矩形一边时,矩形BCQP所在的位置如图所示,直线BC所在的方程为:y=-![]() x-3,则:直线BP的k为-2,所在的方程为y=-2x-3…⑤,
x-3,则:直线BP的k为-2,所在的方程为y=-2x-3…⑤,
联立①⑤解得点P(-4,5),则Q(2,8),即可求解.
:(1)直线y=x-3与坐标轴交于A、B两点,
则A(3,0)B(0,-3),
把B、E点坐标代入二次函数方程,解得:
抛物线的解析式y=![]() x2-x-3…①,
x2-x-3…①,
则:C(6,0);
(2)符合条件的有M和M′,如下图所示,
当∠MBE=75°时,
∵OA=OB,∴∠MBO=30°,
此时符合条件的M只有如图所示的一个点,
MB直线的k为-![]() ,所在的直线方程为:y=-
,所在的直线方程为:y=-![]() x-3…②,
x-3…②,
联立方程①、②可求得:x=4-4![]() ,
,
即:点M的横坐标4-4![]() ;
;
当∠M′BE=75°时,∠OBM′=120°,
直线MB的k值为-![]() ,其方程为y=-
,其方程为y=-![]() x-3,
x-3,
将MB所在的方程与抛物线表达式联立,
解得:x=![]() ,
,
故:即:点M的横坐标4-4![]() 或
或![]() .
.
(3)存在.
①当BC为矩形对角线时,矩形BP′CQ′所在的位置如图所示,
设:P′(m,n),
n=-![]() m2-m-3…③,
m2-m-3…③,
P′C所在直线的k1=![]() ,
,
P′B所在的直线k2=![]() ,则:k1k2=-1…④,
,则:k1k2=-1…④,
③、④联立解得:m=2![]() ,则P′(2
,则P′(2![]() ,3-2
,3-2![]() ),
),
则Q′(6-2![]() ,2
,2![]() -3);
-3);
②当BC为矩形一边时,
情况一:矩形BCQP所在的位置如图所示,
直线BC所在的方程为:y=![]() x-3,
x-3,
则:直线BP的k为-2,所在的方程为y=-2x-3…⑤,
联立①⑤解得点P(-4,5),
则Q(2,8),
情况二:矩形BCP″Q″所在的位置如图所示,
此时,P″在抛物线上,其指标为:(-10,32)..
故:存在矩形,点Q的坐标为:(6-2![]() ,2
,2![]() -3)或(2,8)或(-10,32).
-3)或(2,8)或(-10,32).


科目:初中数学 来源: 题型:
【题目】如图,![]() 是正
是正![]() 内一点,
内一点,![]() ,
,![]() ,
,![]() ,将线段
,将线段![]() 以点
以点![]() 为旋转中心逆时针旋转60°得到线段
为旋转中心逆时针旋转60°得到线段![]() ,连接
,连接![]() ,下列结论:①
,下列结论:①![]() 可以由
可以由![]() 绕点
绕点![]() 逆时针旋转60°得到:②点
逆时针旋转60°得到:②点![]() 与
与![]() 的距离为4;③
的距离为4;③![]() ;④
;④![]() 四边形
四边形![]() ;⑤
;⑤![]() .其中正确的结论是( )
.其中正确的结论是( )
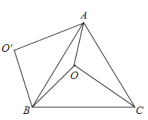
A.①②③④B.①②③⑤C.①②④⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
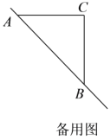
【题目】已知:![]() 是等腰直角三角形,动点
是等腰直角三角形,动点![]() 在斜边
在斜边![]() 所在的直线上,以
所在的直线上,以![]() 为直角边作等腰直角三角形
为直角边作等腰直角三角形![]() ,其中
,其中![]() ,探究并解决下列问题:
,探究并解决下列问题:
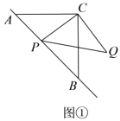
(1)如图①,若点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,则:
,则:
①![]() 长为
长为![]() ;
;![]() 的长为 ;
的长为 ;
②猜想:![]() ,
,![]() ,
,![]() 三者之间的数量关系为 ;
三者之间的数量关系为 ;
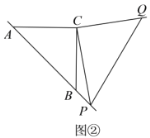
(2)如图②,若点![]() 在
在![]() 的延长线上,在(1)中所猜想的结论依然成立,请你利用图②给出证明过程;
的延长线上,在(1)中所猜想的结论依然成立,请你利用图②给出证明过程;
(3)若动点![]() 满足
满足![]() ,求
,求![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两段材料,回答问题:
材料一:点![]() ,
,![]() 的中点坐标为
的中点坐标为![]() .例如,点
.例如,点![]() ,
,![]() 的中点坐标为
的中点坐标为![]() ,即
,即![]()
材料二:如图1,正比例函数![]() 和
和![]() 的图象相互垂直,分别在
的图象相互垂直,分别在![]() 和
和![]() 上取点
上取点![]() 、
、![]() 使得
使得![]() 分别过点
分别过点![]() 作
作![]() 轴的垂线,垂足分别为点
轴的垂线,垂足分别为点![]() .显然,
.显然,![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,
,![]() ..于是
..于是![]() ,
,![]() 所以
所以![]() 的值为一个常数,一般地,一次函数
的值为一个常数,一般地,一次函数![]() ,
,![]() 可分别由正比例函数
可分别由正比例函数![]() 平移得到.
平移得到.
所以,我们经过探索得到的结论是:任意两个一次函数![]() ,
,![]() 的图象相互垂直,则
的图象相互垂直,则![]() 的值为一个常数.
的值为一个常数.
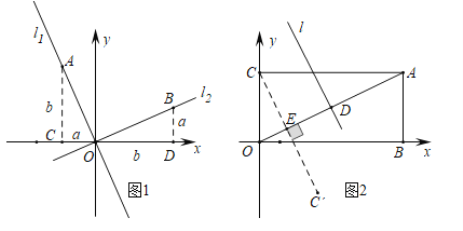
(1)在材料二中,![]() =______(写出这个常数具体的值)
=______(写出这个常数具体的值)
(2)如图2,在矩形![]() 中
中![]() ,点
,点![]() 是
是![]() 中点,用两段材料的结论,求点
中点,用两段材料的结论,求点![]() 的坐标和
的坐标和![]() 的垂直平分线
的垂直平分线![]() 的解析式;
的解析式;
(3)若点![]() 与点
与点![]() 关于
关于![]() 对称,用两段材料的结论,求点
对称,用两段材料的结论,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
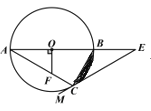
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.
(1)求证:EM是⊙O的切线;
(2)若∠A=∠E,BC=![]() ,求阴影部分的面积.(结果保留
,求阴影部分的面积.(结果保留![]() 和根号).
和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标中,四边形OCNM为矩形,如图1,M点坐标为(m,0),C点坐标为(0,n),已知m,n满足![]() .
.
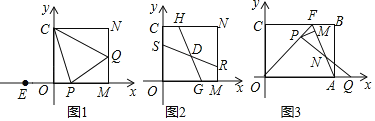
(1)求m,n的值;
(2)①如图1,P,Q分别为OM,MN上一点,若∠PCQ=45°,求证:PQ=OP+NQ;
②如图2,S,G,R,H分别为OC,OM,MN,NC上一点,SR,HG交于点D.若∠SDG=135°,![]() ,则RS=______;
,则RS=______;
(3)如图3,在矩形OABC中,OA=5,OC=3,点F在边BC上且OF=OA,连接AF,动点P在线段OF是(动点P与O,F不重合),动点Q在线段OA的延长线上,且AQ=FP,连接PQ交AF于点N,作PM⊥AF于M.试问:当P,Q在移动过程中,线段MN的长度是否发生变化?若不变求出线段MN的长度;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,⊙O经过A、B两点,且交AC于点D,连接BD,∠DBC=∠BAC.
(1)证明BC与⊙O相切;
(2)若⊙O的半径为6,∠BAC=30°,求图中阴影部分的面积.
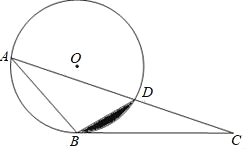
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F分别在平行四边形ABCD边BC和AD上(E、F都不与两端点重合),连结AE、DE、BF、CF,其中AE和BF交于点G,DE和CF交于点H.令![]() ,
,![]() .若
.若![]() ,则图中有_______个平行四边形(不添加别的辅助线);若
,则图中有_______个平行四边形(不添加别的辅助线);若![]() ,且四边形ABCD的面积为28,则四边形FGEH的面积为_______.
,且四边形ABCD的面积为28,则四边形FGEH的面积为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
(1)如果该方程有两个不相等的实数根,求m的取值范围;
(2)在(1)的条件下,当关于x的抛物线![]() 与x轴交点的横坐标都是整数,且
与x轴交点的横坐标都是整数,且![]() 时,求m的整数值.
时,求m的整数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com