
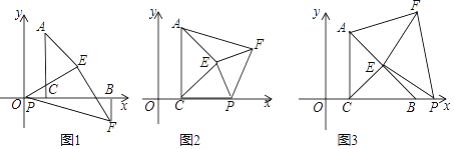
【题目】如图,在△ABC中,点B,C是x轴上的两个定点,∠ACB=90°,AC=BC,点A(l,3),点P是x轴上的一个动点,点E是AB的中点,在△PEF中,∠PEF=90°,PE=EF
(1)如图1,当点P与坐标原点重合时:①求证△PCE≌△FBE;②求点F的坐标;
(2)如图2,当点P在线段CB上时,求证S△CPE=S△AEF
(3)如图3,当点P在线段CB的延长线时,若S△AEF=4S△PBE则此刻点F的坐标为________
【答案】(1)①证明见解析②(4,﹣1)(2)证明见解析(3)(4,4)
【解析】
(1)①只要证明∠OEC=∠FEB,OE=EF,EC=EB,即可解决问题.
②由△PCE≌△FBE推出BF=PC=1,只要证明BF⊥PB即可.
(2)如图2中,作PM⊥CE于M,FN⊥EB于N,根据全等三角形的性质可知PM=FN,由S△CPE=![]() CEPM,S△AEF=
CEPM,S△AEF=![]() AEFN,即可证明.
AEFN,即可证明.
(3)由(2)可知△ECP≌△EBF,推出PC=BF,BF⊥CP,由S△CPE=S△AEF,S△AEF=4S△PBE,推出S△CPE=4S△PBE,推出PC=4PB,推出BC=3PB,PB=1,PC=4,推出BF=PC=4,由此即可解决问题.
(1)证明:如图1中,
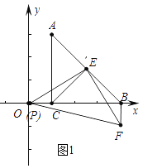
①∵A(1,3),B(4,0),
∴AC=BC=3,△ACB是等腰直角三角形,
∵AE=EB,
∴CE=AE=EB,CE⊥AB,∠ECB=∠EBC=45°,
∴∠CEB=∠OEF=90°,∠ECO=135°,
∴∠OEC=∠FEB,∵OE=EF,EC=EB,
∴△EOC≌△EFB,即△PCE≌△FBE..
②∵△PCE≌△FBE.
∴OC=BF=1,∠EBF=∠OCE=135°,
∴∠OBF=90°,
∴BF⊥OB,
∴F(4,﹣1)
(2)证明:如图2中,作PM⊥CE于M,FN⊥EB于N.
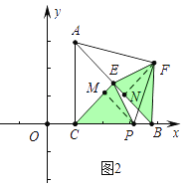
由(1)可知∠OEC=∠FEB,OE=EF,EC=EB,
∴△ECP≌△EBF,
∵PM⊥CE于M,FN⊥EB于N,
∴PM=FN(全等三角形对应边上的高相等),
∵S△CPE=![]() CEPM,S△AEF=
CEPM,S△AEF=![]() AEFN,
AEFN,
∵CE=AE,PM=NF,
∴S△CPE=S△AEF
(3)如图3中,
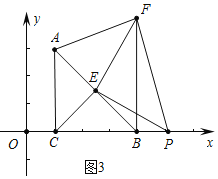
由(2)可知△ECP≌△EBF,推出PC=BF,BF⊥CP,
∵S△CPE=S△AEF,S△AEF=4S△PBE,
∴S△CPE=4S△PBE,
∴PC=4PB,
∴BC=3PB,PB=1,PC=4,
∴BF=PC=4,
∴点F坐标为(4,4).
故答案为(4,4).


科目:初中数学 来源: 题型:
【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.

完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…,根据这个规律,第2 018个点的坐标为( )
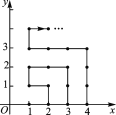
A. (45,9) B. (45,11) C. (45,7) D. (46,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案: ①AD=AE;②BD=CE;③BE=CD;④∠BAD=∠CAE,其中可行的有( )
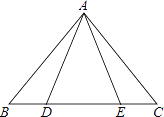
A. 1种 B. 2种 C. 3种 D. 4种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,求∠A的度数.
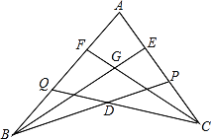
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=![]() ,BE=
,BE=![]() .求CD的长和四边形ABCD的面积.
.求CD的长和四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于H. 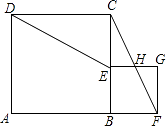
(1)若E是BC的中点,求证:DE=CF;
(2)若∠CDE=30°,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为________________________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com