
分析 (1)根据方程的系数结合根的判别式,即可得出△=(k-3)2≥0,由此即可证出:无论k取任何实数值,方程总有实数根;
(2)由根与系数的关系可得出x1+x2=k+1、x1•x2=2k-2,结合x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=2x1+2x2+8,即可得出关于k的一元二次方程,解之即可得出k的值.
解答 (1)证明:在方程x2-(k+1)x+2k-2=0中,△=[-(k+1)]2-4×(2k-2)=(k-3)2≥0,
∴无论k取任何实数值,方程总有实数根;
(2)解:∵方程的两根分别为x1,x2,
∴x1+x2=k+1,x1•x2=2k-2.
∵x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=(x1+x2)2-2x1•x2=2x1+2x2+8,即(k+1)2-2(2k-2)=2(k+1)+8,
整理得:k2-4k-5=0,
解得:k1=-1或k2=5.
点评 本题考查了根的判别式、根与系数的关系以及解一元二次方程,解题的关键是:(1)熟练掌握“当△≥0时,方程有两个实数根”;(2)根据根与系数的关系结合x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=2x1+2x2+8,找出关于k的一元二次方程.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
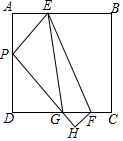 现有边长为4cm的正方形纸片ABCD,点P在AD上,将正方形纸片ABCD折叠使点B落在点P处,点C落在点H处,PH与CD交于点G,折痕为EF,连接EG.
现有边长为4cm的正方形纸片ABCD,点P在AD上,将正方形纸片ABCD折叠使点B落在点P处,点C落在点H处,PH与CD交于点G,折痕为EF,连接EG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,弦CD平分∠ACB,CD交OB于点E.DF⊥AC于点F,交AO于点G.
如图,AB为⊙O的直径,弦CD平分∠ACB,CD交OB于点E.DF⊥AC于点F,交AO于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com