
���� ��1�����Ȱ���������ͨ�֣�Ȼ���ټ����ʽ�ij������Ȱѷ��ӻ��ĸ�ֽ���ʽ��Ȼ��Լ�ֻ��������ѡ����������ֵ��ע��Ҫ��֤��ʽ�����壻
��2���ⲻ��ʽ������Ҫȥ��ĸ����Ҫ©��û�з�ĸ���Ȼ��������ϲ�ͬ�������x��ϵ����Ϊ1��ע�ⲻ��ʽ����ͬʱ����ͬһ��������Ҫ��ţ�
��� �⣺��1��ԭʽ=$\frac{x-1}{x}$��$\frac{{x}^{2}-2x+1}{x}$��
=$\frac{x-1}{x}$•$\frac{x}{��x-1��^{2}}$��
=$\frac{1}{x-1}$��
�������x����ȡ1��0����������xȡ-1��2��
��x=2ʱ��ԭʽ=$\frac{1}{2-1}$=1��
��2���ڢٲ��Ĵ����ǣ�ȥ��ĸʱ��©�˲�����ĸ����-1��
�ڢڲ����ڢ۲��Ĵ����ǣ�����ʽ���߳���-2ʱ�����Ⱥŷ���û�иı䣮
����ʽ����ȷ�⼯Ϊx��$\frac{1}{2}$��
�ʴ�Ϊ��ȥ��ĸʱ��©�˲�����ĸ����-1������ʽ���߳���-2ʱ�����Ⱥŷ���û�иı䣻x��$\frac{1}{2}$��
���� ������Ҫ�����˷�ʽ�Ļ�����ֵ���Լ�һԪһ�β���ʽ�Ľⷨ���Ȱѷ�ʽ������ٰѷ�ʽ��δ֪����Ӧ��ֵ���������ʽ��ֵ���ڻ���Ĺ�����Ҫע������˳��ͷ�ʽ�Ļ��������������ӡ���ĸҪ����Լ�֣�ע������Ľ��Ҫ��������ʽ����ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
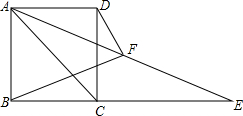 ��ͼ������ABCD������A����DAC�Ľ�ƽ������BC���ӳ����ཻ�ڵ�E��
��ͼ������ABCD������A����DAC�Ľ�ƽ������BC���ӳ����ཻ�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2ax-ax=ax | B�� | x2y-2xy2=-xy2 | C�� | a2+7a2=8a4 | D�� | ��3a��3=9a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
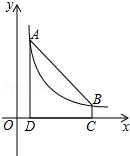 ��ͼ����A��m��6����B��n��1���ڷ���������ͼ���ϣ�AD��x���ڵ�D��BC��x���ڵ�C��
��ͼ����A��m��6����B��n��1���ڷ���������ͼ���ϣ�AD��x���ڵ�D��BC��x���ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com