
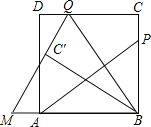
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
【答案】(1)AP=BQ;(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)要证AP=BQ,只需证△PBA≌△QCB即可;
(2)过点Q作QH⊥AB于H,如图.易得QH=BC=AB=3,BP=2,PC=1,然后运用勾股定理可求得AP(即BQ)=![]() ,BH=2.易得DC∥AB,从而有∠CQB=∠QBA.由折叠可得∠C′QB=∠CQB,即可得到∠QBA=∠C′QB,即可得到MQ=MB.设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中运用勾股定理就可解决问题;
,BH=2.易得DC∥AB,从而有∠CQB=∠QBA.由折叠可得∠C′QB=∠CQB,即可得到∠QBA=∠C′QB,即可得到MQ=MB.设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中运用勾股定理就可解决问题;
(3)过点Q作QH⊥AB于H,如图,同(2)的方法求出QM的长,就可得到AM的长.
解:(1)AP=BQ.
理由:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
∴∠ABQ+∠CBQ=90°.
∵BQ⊥AP,∴∠PAB+∠QBA=90°,
∴∠PAB=∠CBQ.
在△PBA和△QCB中,
 ,
,
∴△PBA≌△QCB,
∴AP=BQ;
(2)过点Q作QH⊥AB于H,如图.
∵四边形ABCD是正方形,
∴QH=BC=AB=3.
∵BP=2PC,
∴BP=2,PC=1,
∴BQ=AP=![]() =
=![]() =
=![]() ,
,
∴BH=![]() =
=![]() =2.
=2.
∵四边形ABCD是正方形,
∴DC∥AB,
∴∠CQB=∠QBA.
由折叠可得∠C′QB=∠CQB,
∴∠QBA=∠C′QB,
∴MQ=MB.
设QM=x,则有MB=x,MH=x﹣2.
在Rt△MHQ中,
根据勾股定理可得x2=(x﹣2)2+32,
解得x=![]() .
.
∴QM的长为![]() ;
;
(3)过点Q作QH⊥AB于H,如图.
∵四边形ABCD是正方形,BP=m,PC=n,
∴QH=BC=AB=m+n.
∴BQ2=AP2=AB2+PB2,
∴BH2=BQ2﹣QH2=AB2+PB2﹣AB2=PB2,
∴BH=PB=m.
设QM=x,则有MB=QM=x,MH=x﹣m.
在Rt△MHQ中,
根据勾股定理可得x2=(x﹣m)2+(m+n)2,
解得x=m+n+![]() ,
,
∴AM=MB﹣AB=m+n+![]() ﹣m﹣n=
﹣m﹣n=![]() .
.
∴AM的长为![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD被直线EF所截,∠1=50°,下列说法错误的是( )
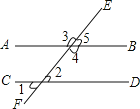
A.如果∠5=50°,那么AB∥CD B.如果∠4=130°,那么AB∥CD
C.如果∠3=130°,那么AB∥CD D.如果∠2=50°,那么AB∥CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).
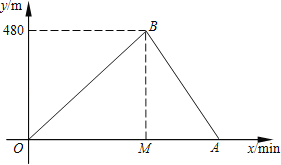
(1)A点所表示的实际意义是 ;![]() = ;
= ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数是( )
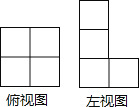
A.5或6或7 B.6或7 C.6或7或8 D.7或8或9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
①﹣10+8
②﹣20+(﹣14)﹣(﹣18)﹣13
③2﹣2÷(﹣![]() )×3
)×3
④﹣14﹣![]() ×[3﹣(﹣3)2]
×[3﹣(﹣3)2]
⑤﹣24×(﹣![]() +
+![]() ﹣
﹣![]() )
)
⑥﹣22+3×(﹣2)﹣(﹣4)2÷(﹣8)﹣(﹣1)100.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的函数表达式为y1=﹣3x+3,且l1与x轴交于点D,直线l2:y2=kx+b经过点A,B,与直线l1交于点C.
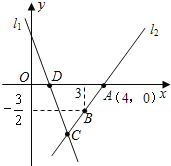
(1)求直线l2的函数表达式及C点坐标;
(2)求△ADC的面积;
(3)当x满足何值时,y1>y2;(直接写出结果)
(4)在直角坐标系中有点E,和A,C,D构成平行四边形,请直接写出E点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com