Question

已知：抛物线y=x²-2x-m（m＞0）与y轴交于点C，C点关于抛物线对称轴的对称点为C′点．
（1）求C点，C′点的坐标（可用含m的代数式表示）；
（2）如果点Q在抛物线的对称轴上，点P在抛物线上，以点C，C′，P，Q为顶点的四边形是平行四边形，求Q点和P点的坐标（可用含m的代数式表示）；
（3）在（2）的条件下，求出平行四边形的周长．

Answer 1

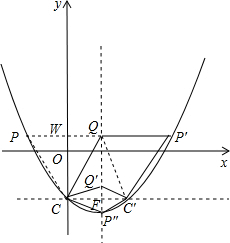
解：（1）所求对称轴为直线x=1，C（0，-m）C′（2，-m）；

（2）如图所示
①当PQ∥CC′且PQ=2时，P横坐标为3，代入二次函数解析式求得P（3，3-m），
②当P′Q∥CC′且PQ=2时，P横坐标为-1，代入二次函数解析式求得P（-1，3-m），
③因为CC′⊥Q'P″，当Q′F=P″F，CF=C'F时，P″为二次函数顶点坐标，为（1，-1-m），
由于P″和Q′关于直线CC′对称，
所以Q′纵坐标为2（-m）+1+m=-m+1，
得Q′（1，1-m），
所以满足条件的P、Q坐标为P（-1，3-m），Q（1，3-m）；P′（3，3-m），Q（1，3-m）；P″（1，-1-m），Q′（1，1-m）．

（3）①因为Q点纵坐标为3-m，C点纵坐标为-m，
所以CW=3-m+m=3，又因为WQ=1，
所以CQ==，
又因为CC′=2，
所以平行四边形CC′P′Q周长为（2+）×2=4+2，
同理，平行四边形CC′QP周长也为4+2．
②因为CF=1，FQ=[1-m-（-1-m）]=1，C′Q==．
平行四边形CC′P′Q周长为4，
所求平行四边形周长为4+2或．
分析：（1）根据抛物线的解析式y=x²-2x-m（m＞0）可求出对称轴直线，令x=0，可求出C点坐标，根据其对称轴可求出C′的坐标．
（2）画出图形，根据平行四边形的性质，令对边平行且相等或对角线互相垂直平分解答．
（3）根据勾股定理求出各边长，即可求出四边形周长．
点评：本题是一道中考压轴题，考查了二次函数图象上点的坐标特征．尤其是（2）题，有一定的开放性，最好是借助图象进行解答．