
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(1,-4) ,B(3,-3) ,C(1,-1).(每个小方格都是边长为一个单位长度的正方形)
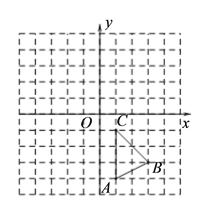
(1)将△ABC沿y轴方向向上平移5个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕点O顺时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点A旋转到点A2所经过的路径长.
【答案】(1)画图见解析;(2)画图见解析,点A旋转到点A2所经过的路径长为![]()
【解析】
(1)按题中要求在平面直角坐标系中画出点A1、B1、C1三点,再顺次连接这三点即可得到所求三角形;
(2)连接OA,在第三象限作OA2⊥OA,并使OA2=OA,即可得到点A2,同法作出点B2、C2,再顺次连接所得三点即可得到所求三角形;由题意和所在图形可知,点A旋转到A2所经过路径的长度是以点O为圆心,OA为半径,圆心角度数为90度的弧的长度,因此根据题中已知条件计算出![]() 的长度即可;
的长度即可;
(1)如下图,△A1B1C1为所求三角形:
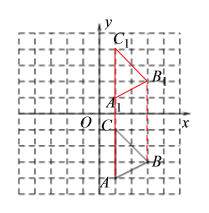
(2)如下图,△A2B2C2为所求三角形:
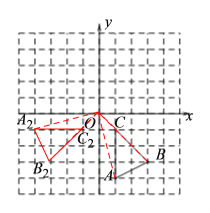
如上图,由题意可知点A旋转到点A2所经过的路径是![]() ,
,
∵OA=![]() ,∠AOA2=90°,
,∠AOA2=90°,
∴![]() .
.
∴点A旋转到点A2所经过的路径长为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
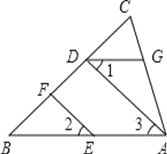
∵EF∥AD,(________)
∴∠2=______.(两直线平行,同位角相等;)
又∵∠1=∠2,(________)
∴∠1=∠3.(________)
∴AB∥DG.(________)
∴∠BAC+______=180°(________)
又∵∠BAC=70°,(________)
∴∠AGD=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个关于数学的故事,蓬蓬国王为了获得贫穷老百的支持,图一个“乐善好施”的好名声,决定施舍每个男人1美元,每个女人0.4美元.为了不使自己花费过多,他想来想去,最后想出了一个方法,决定在正午12时去一个贫困的山村.他十分清楚,在那时,村庄里有60%的男人都外出打猎去了,外出打猎的都不用给钱.已知该村庄里共有1200人,请问:
(1)若该村庄男人共有400人,则国王会用去多少美元?
(2)若该村庄女人共有400人,则国王会用去多少美元?
(3)有人说国王用去的钱数与村庄里男人和女人的具体数目无关,你认为正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个有理数的和等于这两个有理数的积,则称这两个有理数互为相依数.例如:有理数![]() 与3,因为
与3,因为![]() +3=
+3=![]() ×3.所以有理数与
×3.所以有理数与![]() 与3是互为相依数.
与3是互为相依数.
(1)直接判断下列两组有理数是否互为相依数,
①-5与-2;②-3与![]() ;
;
(2)若有理数![]() 与-7 互为相依数,求m的值;
与-7 互为相依数,求m的值;
(3)若有理数a与b互为相依数,b与c互为相反数,求式子5(ab+![]() c)-2(
c)-2(![]() a-b)-4的值;
a-b)-4的值;
(4)对于有理数a(a≠0,1),对它进行如下操作:取a的相依数,得到a1;取a1的倒数,得到a2;取a2的相依数,得到a3;取a3的倒数,得到a4;…,;依次按如上的操作得到一组数a1,a2,a3,…,an , 若a=![]() ,试着直接写出a1,a2,a3,…, a2018的和.
,试着直接写出a1,a2,a3,…, a2018的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
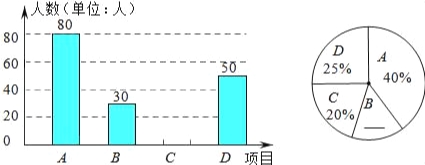
【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设A:踢毽子;B:篮球;C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.
请结合图中的信息解答下列问题:
(1)本次共调查了多少名学生?
(2)请将两个统计图补充完整;
(3)请求出C项目所占的圆心角是 72 度;
(4)若该中学有1200名学生,喜欢篮球运动项目的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 是正方形,
是正方形,![]() 是直线
是直线![]() 上任意一点,
上任意一点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .当点G在BC边上时(如图1),易证DF-BE=EF.
.当点G在BC边上时(如图1),易证DF-BE=EF.

(1)当点![]() 在
在![]() 延长线上时,在图2中补全图形,写出
延长线上时,在图2中补全图形,写出![]() 、
、![]() 、
、![]() 的数量关系,并证明;
的数量关系,并证明;
(2)当点![]() 在
在![]() 延长线上时,在图3中补全图形,写出
延长线上时,在图3中补全图形,写出![]() 、
、![]() 、
、![]() 的数量关系,不用证明.
的数量关系,不用证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E为AB边上一点,DE=DC,点F为线段DE上一点,满足∠DFC=∠A,连结CE.
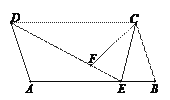
(1)求证:AD=FC;
(2)求证:CE是∠BCF的角平分线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com