
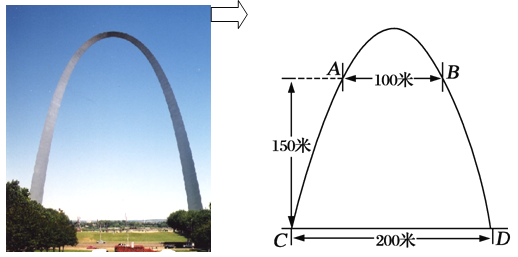
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线![]() 与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
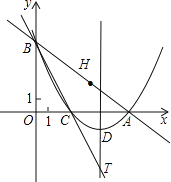
(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;
(2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
(3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA﹣QO|的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
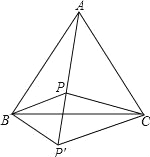
【题目】P为等边△ABC内的一点,PA=10,PB=6,PC=8,将△ABP绕点B顺时针旋转60°到△CBP′位置.
(1)判断△BPP′的形状,并说明理由;
(2)求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种船,1艘大船与4艘小船一次可以载乘客46名,2艘大船与3艘小船一次可以载乘客57人.某船家有3艘大船与6艘小船,一次可以载游客的人数为( )
A.129 B.120 C.108 D.96
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过度包装既浪费资源又污染环境,据测算,如果全国每年减少十分之一的包装纸用量,那么能减少3120000吨二氧化碳的排放量,把数据3120000用科学记数法表示为( )
A. 312×104 B. 3.12×106 C. 0.312×107 D. 3.12×107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com