【题目】甲地与丙地由公路连接，乙地在甲、丙两地之间，一辆汽车在下午1点钟从离甲地10千米的M地出发向乙地匀速前进，15分钟后离甲地20千米，当汽车行驶到离甲地150千米的乙地时，接到通知要在下午5点前赶到离乙地30千米的丙地．汽车若按原速能否按时到达？若能，是在几点几时到达；若不能，车速应提高到多少才能按时到达？
【答案】汽车原速不能按时到达，车速应提高到60千米/小时才能按时到达
【解析】
根据从离甲地10千米的M地出发向乙地匀速前进，15分钟后离甲地20千米可求得汽车的速度为40千米/小时，再求得当汽车行驶到离甲地150千米的乙地时，此时汽车所用的时间为
小时；因接到通知要在下午5点前赶到离乙地30千米的丙地，此时剩时
小时，求得小时汽车原速所走的路程，与30比较即可判定汽车按原速能否按时到达；用30除以即可求得提速后的车速.
∵从离甲地10千米的M地出发向乙地匀速前进，15分钟后离甲地20千米，
∴汽车的速度为：（20-10）÷
=40（千米/小时）；
当汽车行驶到离甲地150千米的乙地时，此时汽车所用的时间为：
（小时）；
因接到通知要在下午5点前赶到离乙地30千米的丙地，此时剩时：5-1-=（小时），
∵40×=20＜30，
∴汽车原速不能按时到达．
∵30÷=60（千米/小时），
∴车速应提高到60千米/小时才能按时到达．
答：汽车原速不能按时到达，车速应提高到60千米/小时才能按时到达．
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB=90°，AC=BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点D，CG平分∠ACB交BD于点G，F为AB边上一点，连接CF，且∠ACF=∠CBG．求证： 
（1）AF=CG；
（2）CF=2DE．
查看答案和解析>>
科目：初中数学 来源： 题型：
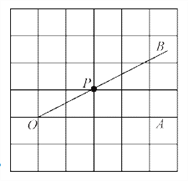
【题目】如图，在
的正方形网格中，点P是
的边OB上的一点．
（1）过点P画OB的垂线，交OA于点C；过点P画OA的垂线，垂足为H；
（2）线段PH的长度是点P到直线__________的距离；
（3）线段__________的长度是点C到直线OB的距离；
（4）线段PC、PH、OC这三条线段大小关系是__________（用“<”号连接）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）单项式﹣2x3ym与5xn+1y的差是一个单项式，求
的值；
（2）化简求值：（x2+5﹣4x3）﹣2（﹣2x3+5x﹣4），其中x=﹣2；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列变形中：
①由方程
=2去分母，得x﹣12=10；
②由方程
x=
两边同除以，得x=1；
③由方程6x﹣4=x+4移项，得7x=0；
④由方程2﹣
两边同乘以6，得12﹣x﹣5=3（x+3）．
错误变形的个数是（ ）个．
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】四边形ABCD中，对角线AC、BD相交于点O，给出下列四组条件：①AB∥CD，AD∥BC；②AB=CD，AD=BC；③AO=CO，BO=DO；④AB∥CD，AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知E、F分别为平行四边形ABCD的对边AD、BC上的点，且DE=BF，EM⊥AC于M，FN⊥AC于N，EF交AC于点O，
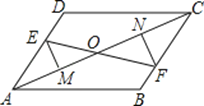
求证：（1）EM=FN；
（2）EF与MN互相平分．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（2，2），B（4，0），C（4，﹣4）． （Ⅰ）请在图中，画出△ABC向左平移6个单位长度后得到的△A1B1C1；
（Ⅱ）以点O为位似中心，将△ABC缩小为原来的 
，得到△A2B2C2 ， 请在图中y轴右侧，画出△A2B2C2 ， 并求出∠A2C2B2的正弦值．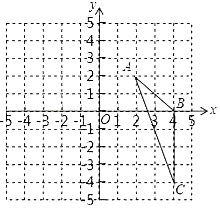
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
