
随州购物中心准备采购数量相同的甲、乙两种衬衫,每件以相同的售价x元出售,其中50≤x≤120,甲种衬衫每件进价为30元,当每件定价为50元时,月销售量为120件,每件售价不超过100元时,价格每上涨1元,每件销量减少1件;售价超过100元时,超过100元的部分,每上涨1元,销量减少2件,销售甲种衬衫的月利润为y1(元),销售乙种衬衫的月利润为y2(元),且y2与x的函数关系为y2=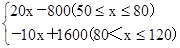 ,销售这两种衬衫的月利润W(元)是y1与y2的和。
,销售这两种衬衫的月利润W(元)是y1与y2的和。
(1)求y1关于x的函数关系式。
(2)求出W关于x的函数关系式。
(3)商场经理如何采购,如何定价,才能使每月获得的总利润W最大?说明理由。
(1)当50≤x≤100时,y1=-x2+200x-5100, 100≤x≤120时,y1=-2x2+330x+8100
(2)50≤x≤80时,W=-x2+220x-5900, 80<x≤100时,W=-x2+190x-3500, 100<x≤120时,W=-2x2+320x-6500(3)甲、乙两种衬衫均采购75件,定价为每件95元,每月获得总利润最大。
【解析】(1)当50≤x≤100时,y1=(x-30)[120-(x-50)]=-x2+200x-5100
100≤x≤120时,y1=(x-30)[120-(100-50)-2(x-100)]=-2x2+330x+8100
(2)50≤x≤80时,W=y1+y2=-x2+220x-5900
80<x≤100时,W=y1+y2=-x2+190x-3500
100<x≤120时,W=y1+y2=-2x2+320x-6500
50≤x≤80时,对和轴x=110,抛物线开口向下
∴50≤x≤80,W随x增大而增大,x=80时,W最大=5300
80≤x≤100时,对称轴x=95,抛物线开口向下
∴x=95时,W最大=5525
100≤x≤120时,对称轴x=80抛物线开口向下
∴100≤x≤120在对称轴右侧,W随x增大而减小
∴x=100时,W最大=5500
∵5525>5500>5300
∴x=95时,最大利润为5525元,销售量为75件
答:甲、乙两种衬衫均采购75件,定价为每件95元,每月获得总利润最大。
(1)根据已知销售价x(元)与销量之间的关系得出x的取值范围;根据x的取值范围得出利润与单价以及销量之间的关系式;
(2)根据y1与y2的函数关系式,得出y1+y2=w,求出即可;
(3)根据自变量的取值范围,分别求出二次函数最值即可.


科目:初中数学 来源:2012届湖北省随州市四校中考模拟联考数学卷(带解析) 题型:解答题
随州购物中心准备采购数量相同的甲、乙两种衬衫,每件以相同的售价x元出售,其中50≤x≤120,甲种衬衫每件进价为30元,当每件定价为50元时,月销售量为120件,每件售价不超过100元时,价格每上涨1元,每件销量减少1件;售价超过100元时,超过100元的部分,每上涨1元,销量减少2件,销售甲种衬衫的月利润为y1(元),销售乙种衬衫的月利润为y2(元),且y2与x的函数关系为y2=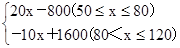 ,销售这两种衬衫的月利润W(元)是y1与y2的和。
,销售这两种衬衫的月利润W(元)是y1与y2的和。
(1)求y1关于x的函数关系式。
(2)求出W关于x的函数关系式。
(3)商场经理如何采购,如何定价,才能使每月获得的总利润W最大?说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com