练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

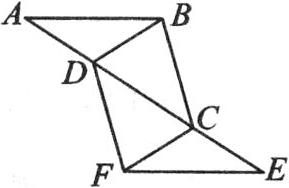
    如图，已知在等腰三角形ABC中，AB=BC，在AC边上取一点D，延长DC至E，使AD=CE，作EF∥AB，EF=AB，连结DF、DB、FC．

    (1)求证：△ABC≌△EFD．

    (2)四边形BDFC是平行四边形吗？若是平行四边形，请证明；若不是，请说明理由．
    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    教材中第25章锐角的三角比，在这章的小结中有如下一段话：锐角三角比定量地描述了在直角三角形中边角之间的联系．在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．
    类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=
    底边
    腰
    =
    BC
    AB
    ．容易知道一个角的大小与这个角的正对值也是相精英家教网互唯一确定的．
    根据上述对角的正对定义，解下列问题：
    （1）sad 60°的值为（　B　）
    A.
    1
    2
    ；B.1；C.
    		3
    2
    ；D.2
    （2）对于0°＜A＜180°，∠A的正对值sad A的取值范围是
     
    ．
    （3）已知sinα=
    3
    5
    ，其中α为锐角，试求sadα的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•奉贤区一模）通过学习锐角三角比，我们知道在直角三角形中，一个锐角的大小与两条边长的比值是一一对应的，因此，两条边长的比值与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做底角的邻对（can），如图（1）在△ABC中，AB=AC，底角B的邻对记作canB，这时canB=
    底边
    腰
    =
    BC
    AB
    ，容易知道一个角的大小与这个角的邻对值也是一一对应的．根据上述角的邻对的定义，解下列问题：
    （1）can30°=
    		3
    		3
    ；
    （2）如图（2），已知在△ABC中，AB=AC，canB=
    8
    5
    ，S△ABC=24，求△ABC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    教材中第25章锐角的三角比，在这章的小结中有如下一段话：锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.

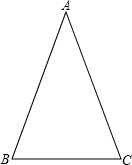
    类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时

    sad A=.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.

    根据上述对角的正对定义，解下列问题：

    （1）sad 的值为（  ▼  ）

     A.             B.1                  C.                  D.2

    （2）对于，∠A的正对值sad A的取值范围是   ▼   .

    （3）已知，其中为锐角，试求sad的值.

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    通过学习锐角三角比，我们知道在直角三角形中，一个锐角的大小与两条边长的比值是一一对应的，因此，两条边长的比值与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做底角的邻对（can），如图（1）在△ABC中，AB=AC，底角B的邻对记作canB，这时canB=数学公式，容易知道一个角的大小与这个角的邻对值也是一一对应的．根据上述角的邻对的定义，解下列问题：
    （1）can30°=______；
    （2）如图（2），已知在△ABC中，AB=AC，canB=数学公式，S△ABC=24，求△ABC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥      AC交AB于点D.

    (1)尺规作图：过A，D，C三点作⊙O（只要求作出图形，  保留痕迹，不要求写作法）；

    (2)求证：BC是过A，D，C三点的圆的切线；

    (3)若过A，D，C三点的圆的半径为,则线段BC上是否存在一点P，使得以P，D，B为顶点的三角

    形与△BCO相似.若存在，求出DP的长；若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案