

分析 (1)利用待定系数法即可解决问题;
(2)如图1中,设C(m,$\frac{12}{m}$).根据题意求出点D坐标,由CD=3,列出方程即可解决问题;
(3)分三种情形讨论①当PC为对角线时,四边形BPQC为平行四边形,②当BC为对角线时,四边形BPCQ为平行四边形,③当PB为对角线时,四边形BQPC为平行四边形,利用平移的性质,求出点Q的坐标,再利用待定系数法即可解决问题;
解答 解:(1)由题意A(8,0),B(0,-4),
∵反比例函数y=$\frac{k}{x}$经过点(-2,-6),
∴k=12,
(2)如图1中,设C(m,$\frac{12}{m}$).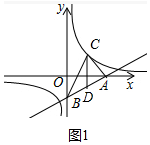
∵CD∥y轴,点D在y=$\frac{1}{2}$x-4上,
∴D(m,$\frac{1}{2}$m-4),
∴CD=$\frac{12}{m}$-($\frac{1}{2}$m-4)=3,
解得m=6或-4(舍弃),
∴C(6,2).
(3)如图2中,设P(n,0).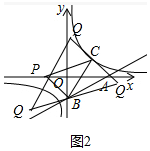
①当PC为对角线时,四边形BPQC为平行四边形,
∴PB∥QC,PB=QC,
∴QC可以看作是由PB平移所得,
∴$\left\{\begin{array}{l}{{x}_{Q}-{x}_{P}={x}_{C}-{x}_{B}}\\{{y}_{Q}-{y}_{P}={y}_{C}-{y}_{B}}\end{array}\right.$,可得$\left\{\begin{array}{l}{{x}_{Q}=n+6}\\{{y}_{Q}=6}\end{array}\right.$,
∴Q(n+6,6),
∵点Q在y=$\frac{12}{x}$上,
∴6(n+6)=12,
∴n=-4,
∴P1(-4,0),Q1(2,6).
②当BC为对角线时,四边形BPCQ为平行四边形,同法可得Q(6-n,-2),
∵点Q在y=$\frac{12}{x}$上,
∴-2(6-n)=12,
∴n=12,
∴P2(12,0),Q2(-6,-2).
③当PB为对角线时,四边形BQPC为平行四边形,同法可得Q(n-6,-6),
∵点Q在y=$\frac{12}{x}$上,
∴-6(n-6)=12,
∴n=4,
∴P3(4,0),Q3(-2,-6),
但是此时P、Q、B、C共线,此种情形不存在.
点评 本题考查反比例函数综合题、一次函数的应用、平行四边形的性质、待定系数法等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考压轴题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
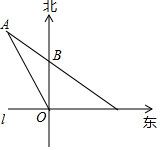 如图,在东西方向的海岸线上有一个码头M,在码头M的正西方向有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距60$\sqrt{3}$千米的A处;经过3小时,又测得该轮船位于O的正北方向,且与O相距60千米的B处.
如图,在东西方向的海岸线上有一个码头M,在码头M的正西方向有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距60$\sqrt{3}$千米的A处;经过3小时,又测得该轮船位于O的正北方向,且与O相距60千米的B处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
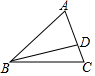 如图,已知在△ABC中,点D在边AC上,CD:AD=1:2,$\overrightarrow{BA}=\overrightarrow{a}$,$\overrightarrow{BC}=\overrightarrow{b}$.
如图,已知在△ABC中,点D在边AC上,CD:AD=1:2,$\overrightarrow{BA}=\overrightarrow{a}$,$\overrightarrow{BC}=\overrightarrow{b}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
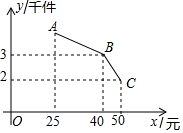 今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队既是联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=-$\frac{1}{20}$x+m(m为常数).
今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队既是联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=-$\frac{1}{20}$x+m(m为常数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com