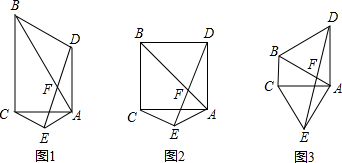
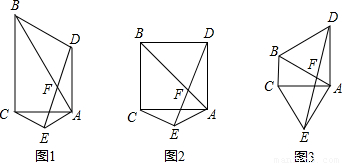
解:(1)∵等腰△ABD和△ACE的顶角∠BAD=∠CAE,
∴AB=AD,AE=AC,∠BAE=∠DAC,
在△ABE和△DAC中,
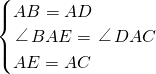
,
∵△ABE≌△ACD(SAS),
∴∠BEA=∠ACD,
∴∠CFE=∠BAD=90゜,
∴∠FBC+∠FCB=90°,
∵BA,CA分别平分∠FBC和∠FCB,
∴∠ABC+∠ACB=45゜,
∵∠DAE=360°-∠BAD-∠CAE-∠BAC=180°-∠BAC,∠BAC=180°-(∠ABC+∠ACB),
∴∠DAE=∠ABC+∠ACB=45゜.
故答案为:45°;
(2)∵等腰△ABD和△ACE的顶角∠BAD=∠CAE,
∴AB=AD,AE=AC,∠BAE=∠DAC,
在△ABE和△DAC中,
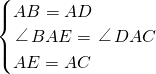
,
∵△ABE≌△ACD(SAS),
∴∠BEA=∠ACD,
∴∠CFE=∠BAD=60゜,
∴∠FBC+∠FCB=60°,
∵BA,CA分别平分∠FBC和∠FCB,
∴∠ABC+∠ACB=30゜,
∵∠DAE=360°-∠BAD-∠CAE-∠BAC=240°-∠BAC,∠BAC=180°-(∠ABC+∠ACB)=150°,
∴∠DAE=90°.
故答案为:90°;
(3)∠DAE=

α-90°.
证明:∵等腰△ABD和△ACE的顶角∠BAD=∠CAE,
∴AB=AD,AE=AC,∠BAE=∠DAC,
在△ABE和△DAC中,
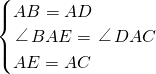
,
∵△ABE≌△ACD(SAS),
∴∠BEA=∠ACD,
∴∠CFE=∠BAD=180°-∠DFE=180°-α,
∴∠FBC+∠FCB=∠EFC=180°-α,
∵BA,CA分别平分∠FBC和∠FCB,
∴∠ABC+∠ACB=

(∠FBC+∠FCB)=90゜-

α,
∴∠BAC=180°-(∠ABC+∠ACB)=90°+

α,
∵∠DAE=360°-∠BAD-∠CAE-∠BAC=

α-90°.
分析:(1)由等腰△ABD和△ACE的顶角∠BAD=∠CAE,可证得△ABE≌△ACD,则可得∠BEA=∠ACD=∠CFE=90゜,继而可得∠ABC+∠ACB=45゜,则可求得∠DAE=45゜;
(2)由等腰△ABD和△ACE的顶角∠BAD=∠CAE,可证得△ABE≌△ACD,则可得∠BEA=∠ACD=∠CFE=60゜,继而可得∠ABC+∠ACB=30゜,则可求得∠DAE=60゜;
(3)由等腰△ABD和△ACE的顶角∠BAD=∠CAE,可证得△ABE≌△ACD,则可得∠BEA=∠ACD=∠CFE=(180-α)゜,继而可得∠ABC+∠ACB=90゜-

α,继而求得答案.
点评:此题考查了全等三角形的判定与性质、角平分线的定义以及三角形外角的性质.此题难度较大,注意掌握数形结合思想的应用.


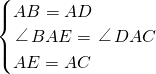 ,
,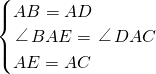 ,
, α-90°.
α-90°.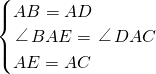 ,
, (∠FBC+∠FCB)=90゜-
(∠FBC+∠FCB)=90゜- α,
α, α,
α, α-90°.
α-90°. α,继而求得答案.
α,继而求得答案.

 走进文言文系列答案
走进文言文系列答案