练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．先化简，再求值：$\frac{1}{4}$（4a2-2a-8）-（$\frac{1}{2}$a-1），其中a=1．

    分析 先化简然后将a的值代入即可求出答案．

    解答 解：当a=1时，
    原式=a2-$\frac{1}{2}$a-2-$\frac{1}{2}$a+1
    =a2-a-1
    =1-1-1
    =-1

    点评 本题考查整式的运算，解题的关键是熟练运用整式的运算法则，本题属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    13．在函数y=$\frac{\sqrt{x-4}}{x-3}$中，自变量x的取值范围是x≥4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．先化简，再求值：x（x+2）+（x-1）（x+1）-2x，其中x=$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

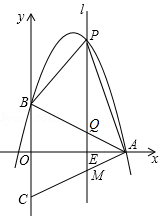    11．如图，在等腰△ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=ax2+$\frac{7}{2}$x+c经过A（8，0）、B（0，4）两点．
    （1）求抛物线的解析式；
    （2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段CA、OA、AB和抛物线于点M、E、Q和点P，连接PA、PB，设直线l移动的时间为t（0＜t＜4）秒，当t为何值时，线段PQ最长？
    （3）在（2）的条件下，抛物线上是否存在一点P，使△PAM的内角为直角？若存在，请直接写出点P的坐标；若不存在，请说明理由．（温馨提示：若直线y=k1x+b1与直线y=k2x+b2垂直，则k1•k2=-1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

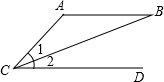    18．如图，有以下3个条件：①AC=AB，②AB∥CD，③∠1=∠2，从这3个条件中任选2个作为题设，另1个作为结论，则组成的命题是真命题的概率是1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．某水果公司购进10 000kg苹果，公司想知道苹果的损坏率，从所有苹果中随机抽取若干进行统计，部分结果如下表：
    苹果总质量n（kg）1002003004005001000
    损坏苹果质量m（kg）10.5019.4230.6339.2449.54101.10
    苹果损坏的频率$\frac{m}{n}$（结果保留小数点后三位）0.1050.0970.1020.0980.0990.101
    估计这批苹果损坏的概率为0.1（结果保留小数点后一位），损坏的苹果约有1000kg．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列计算正确的是（　　）
    A．$\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$B．（-3）2=6C．（-a3）2=a6D．a2+a3=a5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．一个扇形的半径长为5，且圆心角为60°，则此扇形的弧长为$\frac{5}{3}$π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

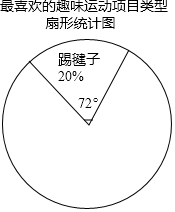    13．某校为更好的开展“冬季趣味运动会”活动，随机在各年级抽查了部分学生，了解他们最喜爱的趣味运动项目类型（跳长绳、踢毽子、背夹球、拔河共四类），并将统计结果绘制成如图不完整的频数分布表．
    根据以上信息回答下列问题：
    最喜爱的趣味运动项目类型频数分布表：
     项目类型 频数频率 
     跳长绳 25 a
     踢毽子 20 0.2
     背夹球 b 0.4
     拔河15  0.15
    （1）直接写出a=0.25，b=40；
    （2）利用频数分布表中的数据，在图中绘制扇形统计图（注明项目、百分比、圆心角）；
    （3）若全校共有学生1200名，估计该校最喜爱背夹球和拔河的学生大约有多少人？

    查看答案和解析>>

    同步练习册答案