
 如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别交于A(-1,0)、B(3,0)、C(0,3)三点.
如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别交于A(-1,0)、B(3,0)、C(0,3)三点.分析 (1)由A、B、C三点的坐标,利用待定系数法可求得抛物线的解析式;
(2)过点P作PD⊥x轴于点D,交BC于点E,PH⊥BC于点H,连结PB、PC,可先求得直线BC的解析式,则可用t分别表示出E的坐标,从而可表示出PE的长,再可用t表示出△PBC的面积,再利用等积法可用t表示出h,利用二次函数的性质可求得h的最大值;
(3)分AM、CM和AC为对角线三种情况,分别根据菱形的性质可求得N点的坐标.
解答 解:
(1)∵抛物线y=ax2+bx+c过A(-1,0)、B(3,0)、C(0,3)三点,
∴$\left\{\begin{array}{l}a-b+c=0\\ 9a+3b+c=0\\ c=3\end{array}\right.$,解得 $\left\{\begin{array}{l}a=-1\\ b=2\\ c=3\end{array}\right.$,
∴抛物线的解析式为y=-x2+2x+3;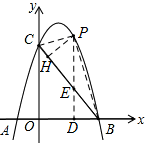
(2)过点P作PD⊥x轴于点D,交BC于点E,PH⊥BC于点H,连结PB、PC.
∵B(3,0)、C(0,3),
∴OB=OC=3,$BC=\sqrt{O{B^2}+O{C^2}}=3\sqrt{2}$,
设直线BC解析式为y=kx+n,则$\left\{\begin{array}{l}3k+n=0\\ n=3\end{array}\right.$,解得 $\left\{\begin{array}{l}k=-1\\ n=3\end{array}\right.$,
∴直线BC解析式为y=-x+3,
∵点P的横坐标为t,且在抛物线y=-x2+2x+3上,
∴P(t,-t2+2t+3),
又∵PD⊥x轴于点D,交BC于点E,
∴D(t,0),E(t,-t+3),
∴PE=(-t2+2t+3)-(-t+3)=-t2+3t,
∴${S_{△PBC}}={S_{△PEB}}+{S_{△PEC}}=\frac{1}{2}PE•BD+\frac{1}{2}PE•OD=\frac{1}{2}PE•(BD+OD)=\frac{1}{2}PE•OB$=$\frac{1}{2}(-{t^2}+3t)×3=-\frac{3}{2}{t^2}+\frac{9}{2}t$,
又∵${S_{△PBC}}=\frac{1}{2}BC•PH=\frac{1}{2}×3\sqrt{2}•h=\frac{{3\sqrt{2}}}{2}h$,
∴$\frac{{3\sqrt{2}}}{2}h=-\frac{3}{2}{t^2}+\frac{9}{2}t$,
∴h与t的函数关系式为:$h=-\frac{{\sqrt{2}}}{2}{t^2}+\frac{{3\sqrt{2}}}{2}t$(0<t<3),
∵$h=-\frac{{\sqrt{2}}}{2}{t^2}+\frac{{3\sqrt{2}}}{2}t=-\frac{{\sqrt{2}}}{2}{(t-\frac{3}{2})^2}+\frac{9}{8}\sqrt{2}$,
∴当$t=\frac{3}{2}$时,h有最大值为$\frac{9}{8}\sqrt{2}$;
(3)存在.
若AM为菱形对角线,则AM与CN互相垂直平分,
∴N(0,-3);
若CM为菱形对角线,则$CN=AM=AC=\sqrt{{1^2}+{3^2}}=\sqrt{10}$,
∴$N(-\sqrt{10},3)$或$N(\sqrt{10},3)$;
若AC为菱形对角线,则CN=AM=CM,
设M(m,0),由CM2=AM2,得m2+32=(m+1)2,解得m=4,
∴CN=AM=CM=5,
∴N(-5,3).
综上可知存在点N,使得以点A、C、M、N为顶点的四边形是菱形,符合条件的点N有4个:N1(0,-3),${N_2}(-\sqrt{10},3)$,${N_3}(\sqrt{10},3)$,N4(-5,3).
点评 本题为二次函数的综合应用,涉及待定系数法、勾股定理、等积法、二次函数的性质、菱形的性质、方程思想和分类讨论思想等知识.在(1)中注意待定系数法的应用,在(2)中用t表示出△PBC的面积是解题的关键,注意等积法的应用,在(3)中注意菱形性质的应用.本题考查知识点较多,综合性较强,难度较大.


科目:初中数学 来源: 题型:选择题
| A. | 2x-x=2 | B. | (x3)3=x6 | C. | |π-2$\sqrt{3}$|=2$\sqrt{3}$-π | D. | x2÷x3=x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DE⊥AB,垂足为E,点B′在边AB上,且与点B关于直线DE对称,连接CB′,当△AB′C为等腰三角形时,BD的长$\frac{5}{2}$或$\frac{7}{4}$或$\frac{25}{8}$.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DE⊥AB,垂足为E,点B′在边AB上,且与点B关于直线DE对称,连接CB′,当△AB′C为等腰三角形时,BD的长$\frac{5}{2}$或$\frac{7}{4}$或$\frac{25}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
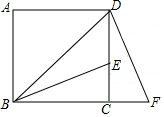 如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC与点E,将△BCE绕点C按顺时针旋转90°得到△DCF,若CE=3cm,则FB=(6+3$\sqrt{2}$)cm.
如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC与点E,将△BCE绕点C按顺时针旋转90°得到△DCF,若CE=3cm,则FB=(6+3$\sqrt{2}$)cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com