
【题目】已知,如图,△ABC,∠ACB=90°,∠B=2∠A.
(1)用直尺和圆规作△ABC的角平分线BD,保留作图痕迹;
(2)在(1)的基础上,求∠ADB的度数.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】某校举办“红歌伴我成长”歌咏比赛活动,参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如图:
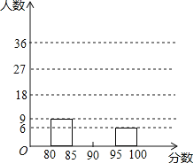
分数段 | 频数 | 频率 |
80≤x<85 | 9 | 0.15 |
85≤x<90 | m | 0.45 |
90≤x<95 | ■ | ■ |
95≤x<100 | 6 | n |
(1)求m,n的值分别是多少;
(2)请在图中补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市举办的“读好书,讲礼仪”活动中,东华学校积极行动,各班图书角的新书、好书不断增多,除学校购买外,还有师生捐献的图书.下面是七年级(1)班全体同学捐献图书的情况统计图:
请你根据以上统计图中的信息,解答下列问题:
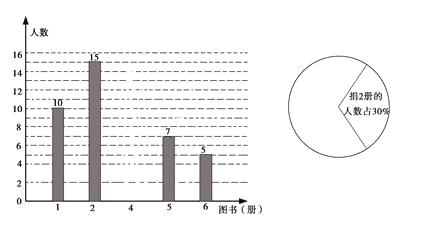
(1)该班有学生多少人?
(2)补全条形统计图;
(3)七(1)班全体同学所捐献图书的中位数和众数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
在上学期的学习中,我们知道若![]() ,其中a是底数,n是指数,m称为幂,知道a和n可以求m.我们不妨思考:如果知道a,m,能否求n呢?对于
,其中a是底数,n是指数,m称为幂,知道a和n可以求m.我们不妨思考:如果知道a,m,能否求n呢?对于![]() ,规定[a,m]=n,例如:
,规定[a,m]=n,例如:![]() ,所以[6,36]=2.
,所以[6,36]=2.
(1)根据上述规定,填空:[3,______]= 4,[2,32]=_____,[-4,1]=______,[5,0.2]=______;
(2)记![]() ,
,![]() ,求y与x之间的关系式.
,求y与x之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
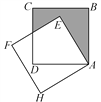
【题目】如图,将边为![]() 的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
A. ![]() -
-![]() B. 3-
B. 3-![]() C. 2-
C. 2-![]() D. 2-
D. 2-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
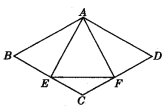
【题目】已知:如图所示,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
(1)试说明:AE=AF;
(2)若∠B=60°,点E,F分别为BC和CD的中点,试说明:△AEF为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1,固定△ABC不动,将△DEF进行如下操作: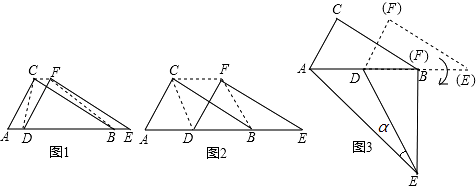
(1)操作发现
如图①,△DEF沿线段AB向右平移(即D点在线段AB内移动),连接DC、CF、FB,四边形CDBF的形状在不断变化,但它的面积不变化,请求出其面积.
(2)猜想论证
如图②,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.
(3)拓展研究
如图③,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB的边上,此时F点恰好与B点重合,连接AE,则sinα= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com