
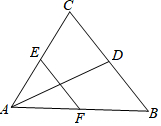
 已知:如图,在△ABC中,D、E、F是分别是三边BC、AC、AB的中点,连接EF、AD.
已知:如图,在△ABC中,D、E、F是分别是三边BC、AC、AB的中点,连接EF、AD.分析 (1)连接DE、DF,只要证明四边形AEDF是平行四边形即可;
(2)当∠BAC=90°时,AD=EF.理由矩形的性质即可证明;
解答 (1)证明:连接DE、DF.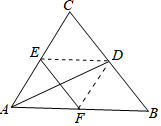
∵D、E、F是分别是三边BC、AC、AB的中点,
∴DE、DF是△ABC的中位线.
∴DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形.
∴AD与EF互相平分.
(2)当∠BAC=90°时,AD=EF.
理由:∵四边形AEDF是平行四边形,且∠BAC=90°,
∴四边形AEDF是矩形,
∴AE=DF.
点评 本题考查三角形的中位线定理、平行四边形的判定和性质、矩形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题.


科目:初中数学 来源: 题型:解答题
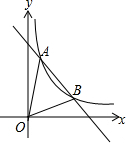 如图,已知反比例函数y=kx-1(k>0)的图象与一次函数图象y=-x+4交于a、b两点,点a的纵坐标为3.
如图,已知反比例函数y=kx-1(k>0)的图象与一次函数图象y=-x+4交于a、b两点,点a的纵坐标为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
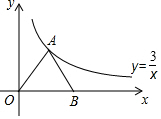 已知反比例函数y=$\frac{3}{x}$在第一象限的图象如图所示,点A是在其图象上,点B为x轴正半轴上一点,连接AO、AB,且AO=AB,则S△AOB=3.
已知反比例函数y=$\frac{3}{x}$在第一象限的图象如图所示,点A是在其图象上,点B为x轴正半轴上一点,连接AO、AB,且AO=AB,则S△AOB=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
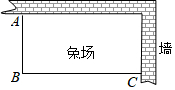 某家庭农场要建一个长方形的养兔场,兔场的两边靠墙(两堵墙互相垂直,长度不限),另两边用木栏围成,木栏总长20米.
某家庭农场要建一个长方形的养兔场,兔场的两边靠墙(两堵墙互相垂直,长度不限),另两边用木栏围成,木栏总长20米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
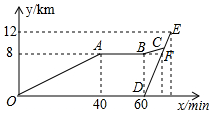 五一假期,小明骑自行车到松花江边游玩,从家出发40min后到达江边大塔,游玩一段时间后按原速度继续前往码头,在小明出发60min后,爸爸驱车沿相同路线前往码头,行驶8min时恰好经过江边大塔,如图是他们离开家的路程y(单位:km)关于小明离家时间x(单位:min)的函数图象.
五一假期,小明骑自行车到松花江边游玩,从家出发40min后到达江边大塔,游玩一段时间后按原速度继续前往码头,在小明出发60min后,爸爸驱车沿相同路线前往码头,行驶8min时恰好经过江边大塔,如图是他们离开家的路程y(单位:km)关于小明离家时间x(单位:min)的函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com