
°æƒø°ø…·¿˚…˙…˙À˛Œª”⁄Ω˙ÏÙƒœ»£¨Ω®”⁄ÀÂø™ª ƒÍº‰£¨ÀŒ¥˙÷ÿ–Þ£¨«Â«¨¬° Æ¡˘ƒÍ£®1751ƒÍ£©÷ÿΩ®£Æ∆þŒð∞ÀΩ«£¨¡¡ßÕþ∂•£¨‘∂‘∂Õ˚»•£¨∏þÀ µƒπ≈À˛£¨”≥≥ƒ◊≈¿∂ÃÏ∞◊‘∆£¨…ı «◊≥π€£Æ‘≠À˛ƒ⁄√ø≤„æ˘”–∑œÒ£¨ø™4√≈8¥∞£¨∆æ¥∞‘∂Ø£¨Ω˙ÏÙƒ⁄Õ‚√¿æ∞ø…“ª¿¿ŒÞ”ý£Æ»Áπ˚‘⁄œ¶—ÙŒ˜œ¬ ±–¿…Õ±¶À˛£¨ªπª·≥ˆœ÷°™°™ÃÏ‘∆Ωı°¢¬˙À˛π‚ª‘µƒ◊≥¿ˆæ∞π€£¨±ª”˛Œ™°∞±¶À˛≈˚œº°±£Æƒ≥ ˝—ß°∞◊€∫œ”Î µº˘°±–°◊ȵƒÕ¨—ß∞—°∞≤‚¡ø…·¿˚…˙…˙À˛∏þ°±◊˜Œ™“ªœÓøŒÃ‚ªÓ∂Ø£¨À˚√«÷∆∂®¡À≤‚¡ø∑Ω∞∏£¨≤¢¿˚”√øŒ”ý ±º‰ÕÍ≥…¡À µµÿ≤‚¡ø£¨≤‚¡øΩ·π˚»Á±Ì£∫
øŒÃ‚ | ≤‚¡ø…·¿˚…˙…˙À˛∏þ | |||
≤‚¡ø æ“‚Õº |
| Àµ√˜£∫ƒ≥Õ¨—ß‘⁄µÿ√Ê…œ—°‘Òµ„C£¨ π”√ ÷≥÷≤‚Ω«“«£¨≤‚µ√¥À ±¬•∂•Aµƒ—ˆΩ«°œAHE£Ω¶¡£¨—ÿCB∑ΩœÚ«∞Ω¯µΩµ„D£¨≤‚¡ø≥ˆC£¨D÷ƺ‰µƒæý¿ÎCD£Ωxm£¨‘⁄µ„D π”√ ÷≥÷≤‚Ω«“«£¨≤‚µ√¥À ±¬•∂•Aµƒ—ˆΩ«°œAFE£Ω¶¬ | ||
≤‚¡ø ˝æð | ¶¡µƒ∂» ˝ | ¶¬µƒ∂» ˝ | CDµƒ≥§∂» | ∏√Õ¨—ß—€æ¶¿Îµÿ√ʵƒæý¿ÎHC |
24°„ | 37°„ | 32m | 1.76m | |
°≠ | °≠ | |||
£®1£©«Î∞Ô÷˙∏√–°◊ȵƒÕ¨—ß∏˘æð…œ±Ì÷–µƒ≤‚¡ø ˝æ𣨫ÛÀ˛∏þAB£Æ£®Ω·π˚æ´»∑µΩ1m£ª≤Œøº ˝æð£∫sin24°„°÷0.41£¨cos24°„°÷0.91£¨tan24°„°÷0.45£¨sin37°„°÷0.60£¨cos37°„°÷0.80£¨tan37°„°÷0.75£©
£®2£©∏√–°◊È“™–¥≥ˆ“ª∑ðÕÍ’˚µƒøŒÃ‚ªÓ∂ر®∏Ê£¨≥˝…œ±Ì÷–µƒœÓƒøÕ‚£¨ƒ„»œŒ™ªπ–Ë“™≤π≥‰ƒƒ–©œÓƒø£ø£®–¥≥ˆ“ª∏ˆº¥ø…£©

°æ¥∞∏°ø£®1£©‘ºŒ™38m£ª£®2£©ªπ–Ë“™≤π≥‰µƒœÓƒøŒ™£∫º∆À„π˝≥㨻À‘±∑÷𧣨÷∏µºΩà ¶£¨ªÓ∂Ø∏– е»£Æ£®¥∞∏≤ªŒ®“ª£¨∫œ¿Ìº¥ø…£Æ£©
°æΩ‚Œˆ°ø
£®1£©“◊÷™Àƒ±þ–ŒHCDF «æÿ–Œ£¨Àƒ±þ–ŒFDBE «æÿ–Œ£¨Ω·∫œ»˝Ω«∫Ø ˝µƒ∂®“«Û≥ˆAE∫ÕBE≥§º¥ø…µ√≥ˆ¥∞∏£ª
£®2£©»Á“™≤π≥‰£∫º∆À„π˝≥㨻À‘±∑÷𧣨÷∏µºΩà ¶£¨ªÓ∂Ø∏– е»£Æ£®¥∞∏≤ªŒ®“ª£¨∫œ¿Ìº¥ø…£Æ£©
Ω‚£∫£®1£©‘⁄Rt°˜AFE÷–£¨tan°œAFE£Ω![]() £¨°œAFE£Ω37°„£¨
£¨°œAFE£Ω37°„£¨
°ý![]() £¨
£¨
°þ°œHCD£Ω90°„£¨°œFDC£Ω90°„£¨
°ýHC°ŒFD£¨
”÷°þHC£ΩFD£¨
°ýÀƒ±þ–ŒHCDF «æÿ–Œ£¨
°ýHF£ΩCD£Ω32m£Æ
‘⁄Rt°˜AHE÷–£¨tan°œAHE£Ω![]() £Ω
£Ω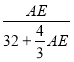 °÷0.45£¨
°÷0.45£¨
Ω‚µ√£∫AE£Ω36£Æ
Õ¨¿Ì£¨Àƒ±þ–ŒFDBE «æÿ–Œ£¨‘ÚBE£ΩFD£ΩHC£Ω1.76m£¨
°ýAB£ΩAE+BE£Ω36+1.76=37.76°÷38£®m£©£Æ
¥£∫À˛∏þAB‘ºŒ™38m£Æ
£®2£©ªπ–Ë“™≤π≥‰µƒœÓƒøŒ™£∫º∆À„π˝≥㨻À‘±∑÷𧣨÷∏µºΩà ¶£¨ªÓ∂Ø∏– е»£Æ£®¥∞∏≤ªŒ®“ª£¨∫œ¿Ìº¥ø…£Æ£©



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂‘”⁄≈◊ŒÔœþy£Ωx2©Å2mx+m2+m©Å2£¨µ±©Å1°Ðx°Ð2 ±£¨∫Ø ˝µƒ◊Ó–°÷µŒ™m£¨‘Úmµƒ÷µŒ™£® £©
A.![]() ªÚ
ªÚ![]() B.
B.![]() ªÚ
ªÚ![]()
C.![]() ªÚ
ªÚ![]() D.
D.![]() ªÚ
ªÚ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
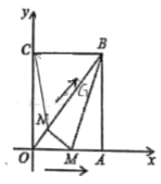
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨“—÷™æÿ–Œ![]() µƒ∂•µ„
µƒ∂•µ„![]() £¨∂ص„
£¨∂ص„![]() £¨
£¨![]() Õ¨ ±¥”
Õ¨ ±¥”![]() µ„≥ˆ∑¢£¨µ„
µ„≥ˆ∑¢£¨µ„![]() —ÿ…‰œþ
—ÿ…‰œþ![]() ∑ΩœÚ“‘√ø√Î
∑ΩœÚ“‘√ø√Î![]() ∏ˆµ•ŒªµƒÀŸ∂»‘À∂Ø£¨µ„
∏ˆµ•ŒªµƒÀŸ∂»‘À∂Ø£¨µ„![]() —ÿœþ∂Œ
—ÿœþ∂Œ![]() ∑ΩœÚ“‘√ø√Î
∑ΩœÚ“‘√ø√Î![]() ∏ˆµ•ŒªµƒÀŸ∂»‘À∂Ø£¨µ±µ„
∏ˆµ•ŒªµƒÀŸ∂»‘À∂Ø£¨µ±µ„![]() µΩ¥Ôµ„
µΩ¥Ôµ„![]() ±£¨µ„
±£¨µ„![]() £¨
£¨![]() Õ¨ ±Õ£÷π‘À∂Ø£¨¡¨Ω”
Õ¨ ±Õ£÷π‘À∂Ø£¨¡¨Ω”![]() £¨…Ë‘À∂Ø ±º‰Œ™
£¨…Ë‘À∂Ø ±º‰Œ™![]() £®√Σ©£Æ
£®√Σ©£Æ
£®1£©«Û÷§![]() £ª
£ª
£®2£©µ±µ„![]() ‘À∂ØµΩµ„
‘À∂ØµΩµ„![]() ±£¨»ÙÀ´«˙œþ
±£¨»ÙÀ´«˙œþ![]() µƒÕºœÛ«°∫√π˝µ„
µƒÕºœÛ«°∫√π˝µ„![]() £¨ ‘«Û
£¨ ‘«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®3)¡¨Ω”![]() £¨µ±
£¨µ±![]() Œ™∫Œ÷µ ±£¨
Œ™∫Œ÷µ ±£¨![]() Œ™µ»—¸»˝Ω«–Œ£Æ
Œ™µ»—¸»˝Ω«–Œ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Rt°˜ACB÷–£¨°œC=90°„£¨AC=3£¨BC=4£¨O «BCµƒ÷–µ„£¨µΩµ„Oµƒæý¿Îµ»”⁄![]() BCµƒÀ˘”–µ„◊È≥…µƒÕº–Œº«Œ™G£¨Õº–ŒG”ÎABΩª”⁄µ„D£Æ
BCµƒÀ˘”–µ„◊È≥…µƒÕº–Œº«Œ™G£¨Õº–ŒG”ÎABΩª”⁄µ„D£Æ

£®1£©≤π»´Õº–Œ≤¢«Ûœþ∂ŒADµƒ≥§£ª
£®2£©µ„E «œþ∂ŒAC…œµƒ“ªµ„£¨µ±µ„E‘⁄ ≤√¥Œª÷√ ±£¨÷±œþED”Î Õº–ŒG”–«“÷ª”–“ª∏ˆΩªµ„£ø«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
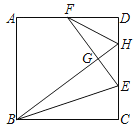
°æƒø°ø»ÁÕº£¨’˝∑Ω–Œ÷Ω∆¨ABCD—ÿ÷±œþBE’€µ˛£¨µ„C«°∫√¬‰‘⁄µ„G¥¶£¨¡¨Ω”BG≤¢—”≥§£¨ΩªCD”⁄µ„H£¨—”≥§EGΩªAD”⁄µ„F£¨¡¨Ω”FH£Æ»ÙAF£ΩFD£Ω6cm£¨‘ÚFHµƒ≥§Œ™_____cm£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
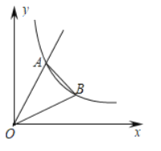
°æƒø°ø»ÁÕº£¨’˝±»¿˝∫Ø ˝y1£Ωk1xµƒÕºœÛ”Î∑¥±»¿˝∫Ø ˝y2£Ω![]() £®x£æ0£©µƒÕºœÛœýΩª”⁄µ„A£®
£®x£æ0£©µƒÕºœÛœýΩª”⁄µ„A£®![]() £¨2
£¨2![]() £©£¨µ„B «∑¥±»¿˝∫Ø ˝ÕºœÛ…œ“ªµ„£¨À¸µƒ∫·◊¯±Í «3£¨¡¨Ω”OB£¨AB£¨‘Ú°˜AOBµƒ√ʪ˝ «_____£Æ
£©£¨µ„B «∑¥±»¿˝∫Ø ˝ÕºœÛ…œ“ªµ„£¨À¸µƒ∫·◊¯±Í «3£¨¡¨Ω”OB£¨AB£¨‘Ú°˜AOBµƒ√ʪ˝ «_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷±œþy£Ω©Å![]() x+b∑÷±”Îx÷·°¢y÷·Ωª”⁄µ„A°¢B£¨«“µ„Aµƒ◊¯±ÍŒ™£®4£¨0£©£¨Àƒ±þ–ŒABCD «’˝∑Ω–Œ£Æ
x+b∑÷±”Îx÷·°¢y÷·Ωª”⁄µ„A°¢B£¨«“µ„Aµƒ◊¯±ÍŒ™£®4£¨0£©£¨Àƒ±þ–ŒABCD «’˝∑Ω–Œ£Æ

£®1£©ÃÓø’£∫b£Ω°° °°£ª
£®2£©«Ûµ„Dµƒ◊¯±Í£ª
£®3£©µ„M «œþ∂ŒAB…œµƒ“ª∏ˆ∂ص„£®µ„A°¢B≥˝Õ‚£©£¨ ‘ÃΩÀ˜‘⁄x…œ∑Ω «∑ҥʑ⁄¡Ì“ª∏ˆµ„N£¨ πµ√“‘O°¢B°¢M°¢NŒ™∂•µ„µƒÀƒ±þ–Œ «¡‚–Œ£ø»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£ª»Ù¥Ê‘⁄£¨«Î«Û≥ˆµ„Nµƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™Ω¯“ª≤Ω∑¢’πª˘¥°ΩÔ˝£¨◊‘2014ƒÍ“‘¿¥£¨ƒ≥œÿº”¥Û¡ÀΩÔ˝æ≠∑—µƒÕ∂»Î£¨2014ƒÍ∏√œÿÕ∂»ÎΩÔ˝æ≠∑—6000ÕÚ‘™°£2016ƒÍÕ∂»ÎΩÔ˝æ≠∑—8640ÕÚ‘™°£ºŸ…Ë∏√œÿ’‚¡ΩƒÍÕ∂»ÎΩÔ˝æ≠∑—µƒƒÍ∆Ωæ˘‘ˆ≥§¬ œýÕ¨°£
£®1£©«Û’‚¡ΩƒÍ∏√œÿÕ∂»ÎΩÔ˝æ≠∑—µƒƒÍ∆Ωæ˘‘ˆ≥§¬ £ª
£®2£©»Ù∏√œÿΩÔ˝æ≠∑—µƒÕ∂»ÎªπΩ´±£≥÷œýÕ¨µƒƒÍ∆Ωæ˘‘ˆ≥§¬ £¨«Îƒ„‘§À„2017ƒÍ∏√œÿÕ∂»ÎΩÔ˝æ≠∑—∂ý…ŸÕÚ‘™°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£Ω´æŸ∞Ï°∞–ƒª≥∏–∂˜°§–¢æ¥∏∏ƒ∏°±µƒªÓ∂Ø£¨Œ™¥À£¨–£—ß…˙ª·æÕ»´–£1 000√˚Õ¨—ß ÓºŸ∆⁄º‰∆Ωæ˘√øÃÏ◊ˆº“ŒÒªÓµƒ ±º‰£¨Àʪ˙≥È»°≤ø∑÷Õ¨—ßΩ¯––µ˜≤È£¨≤¢ªÊ÷∆≥…»Áœ¬Ãı–ŒÕ≥º∆Õº£Æ
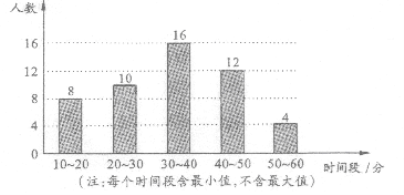
£®1£©±æ¥Œµ˜≤È≥È»°µƒ»À ˝Œ™_______£¨π¿º∆»´–£Õ¨—ß‘⁄ ÓºŸ∆⁄º‰∆Ωæ˘√øÃÏ◊ˆº“ŒÒªÓµƒ ±º‰‘⁄40∑÷÷”“‘…œ(∫¨40∑÷÷”)µƒ»À ˝Œ™_______£ª
£®2£©–£—ß…˙ª·ƒ‚‘⁄±Ìœ÷Õª≥ˆµƒº◊°¢““°¢±˚°¢∂°Àƒ√˚Õ¨—ß÷–£¨Àʪ˙≥È»°¡Ω√˚Õ¨—ߜڻ´–£ª„±®£Æ«Î”√ ˜◊¥ÕºªÚ¡–±Ì∑®±Ì æ≥ˆÀ˘”–ø…ƒÐµƒΩ·π˚£¨≤¢«Û«°∫√≥ÈµΩº◊°¢““¡Ω√˚Õ¨—ßµƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com