
【题目】正方形![]() 、正方形
、正方形![]() 和正方形
和正方形![]() 的位置如图所示,点
的位置如图所示,点![]() 在线段
在线段![]() 上,正方形
上,正方形![]() 的边长为4,则
的边长为4,则![]() 的面积为( )
的面积为( )
A. 10 B. 12 C. 14 D. 16
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).
(1)求抛物线的表达式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BCD的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,N是线段EF上一动点,M(m,0)是x轴上一动点,若∠MNC=90°,直接写出实数m的取值范围.
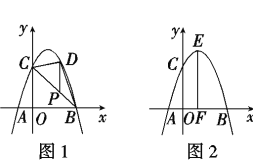
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于50元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每周的利润恰好是2145元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(m+1)x+m2+2=0.
(1)若方程总有两个实数根,求m的取值范围;
(2)若方程有一个实数根为1,求m的值和另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米, ![]() =1.732).
=1.732).

A. 585米 B. 1014米 C. 805米 D. 820米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60km/h(即![]() m/s),交通管理部门在离该公路100m处设置了一速度检测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西60°方向上,点C在点A的北偏东45°方向上.
m/s),交通管理部门在离该公路100m处设置了一速度检测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西60°方向上,点C在点A的北偏东45°方向上.
(1)在图中直接标出表示60°和45°的角;
(2)写出点B、点C坐标;
(3)一辆汽车从点B匀速行驶到点C所用时间为15s.请你通过计算,判断该汽车在这段限速路上是否超速?(本小问中![]() 取1.7)
取1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
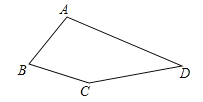
【题目】如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.
(1)求∠A+∠C的度数;
(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;
(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解一路段车辆行驶速度的情况,交警统计了该路段上午7::0至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数、中位数分别是( )
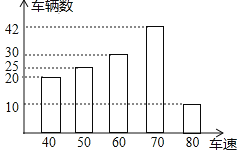
A. 众数是80千米![]() 时,中位数是60千米
时,中位数是60千米![]() 时
时
B. 众数是70千米![]() 时,中位数是70千米
时,中位数是70千米![]() 时
时
C. 众数是60千米![]() 时,中位数是60千米
时,中位数是60千米![]() 时
时
D. 众数是70千米![]() 时,中位数是60千米
时,中位数是60千米![]() 时
时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com