
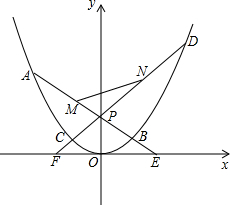
 抛物线C0的顶点为原点O,且过点G(2,1).如图,过点P(0,2)分别作两条直线,l1:y=k1x+2和l2:y=k2x+2(其中k1•k2≠0),两直线分别与抛物线、x轴相交于点A、B、E和D、C、F,且M、N分别是AB、CD的中点.
抛物线C0的顶点为原点O,且过点G(2,1).如图,过点P(0,2)分别作两条直线,l1:y=k1x+2和l2:y=k2x+2(其中k1•k2≠0),两直线分别与抛物线、x轴相交于点A、B、E和D、C、F,且M、N分别是AB、CD的中点.分析 (1)根据抛物线C0的顶点为原点O,且过点G(2,1),利用待定系数法可求得其解析式;
(2)根据两直线的解析式可求得E、F的坐标,在Rt△PEF中,可证明△POF∽△EOP,则可得到PO2=OE•OF,则可得到k1、k2之间的关系;
(3)可设A(a,m),B(b,n),由条件可得到a=-2b,再结合A、B分别在抛物线和直线l1上,则可得到关于x的一元二次方程,利用根与系数的关系,则可求得M点的横坐标,当k1+k2=0时,可知两直线关于y轴对称,可知MN⊥y轴,则可求得MN的长.
解答 解:
(1)∵抛物线C0的顶点为原点O,
∴设抛物线解析式为y=ax2,
把G(2,1)代入得:a=$\frac{1}{4}$,
∴抛物线C0的解析式为y=$\frac{1}{4}$x2;
(2)在y=k1x+2中,令y=0,可得x=-$\frac{2}{{k}_{1}}$,
∴E(-$\frac{2}{{k}_{1}}$,0),
则理可求得F(-$\frac{2}{{k}_{2}}$,0),
∵l1⊥l2,
∴△POF∽△EOP,
∴$\frac{PO}{OE}$=$\frac{OF}{PO}$,
∴PO2=OE•OF,
不妨设k1<0,则k2>0,
∴22=$\frac{2}{{k}_{1}}$•$\frac{2}{{k}_{2}}$,
∴k1•k2=-1;
(3)不妨设k1<0,设A(a,m),B(b,n),
∵PA=2PB,
∴a=-2b①,
由点A、B分别在抛物线和直线l1上,联立$\left\{\begin{array}{l}{y=\frac{1}{4}{x}^{2}}\\{y={k}_{1}x+2}\end{array}\right.$,整理可得x2-4k1x-8=0,
∴ab=-8②,
由①②可得a=-4,b=2,
∵M为AB的中点,
∴M横坐标为-1,
当k1+k2=0时,由(2)可知l1和l2关于y轴对称,
∵M、N关于y轴对称,
∴N点横坐标为1,
∴MN=1-(-1)=2.
点评 本题为二次函数的综合应用,涉及待定系数法、相似三角形的判定和性质、一元二次方程根与系数的关系、中点的定义及方程思想等知识.在(1)中注意抛物线解析式的形式,在(2)中利用相似三角形的性质得到k1、k2的关系是解题的关键,在(3)中求得M、N的横坐标是解题的关键,注意利用k1+k2=0.本题考查知识点较多,综合性较强,难度适中.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:选择题
| A. | 无数次实验后,该事件发生的频率逐渐稳定在$\frac{1}{4}$左右 | |
| B. | 无数次实验中,该事件平均每4次出现1次 | |
| C. | 每做4次实验,该事件就发生1次 | |
| D. | 逐渐增加实验次数,该事件发生的频率就和$\frac{1}{4}$逐渐接近 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | 0 | 2 | 3 |
| y | 0.37 | 0.37 | 4 |
| A. | 20 | B. | 8 | C. | 24 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
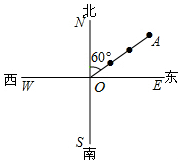 如图,货轮O在航行过程中,在它的北偏东60°方向上,与之相距30海里处发现灯塔A,同时在它的南偏东30°方向上,与之相距20海里处发现货轮B,在它的西南方向上发现客轮C,按下列要求画出.
如图,货轮O在航行过程中,在它的北偏东60°方向上,与之相距30海里处发现灯塔A,同时在它的南偏东30°方向上,与之相距20海里处发现货轮B,在它的西南方向上发现客轮C,按下列要求画出.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
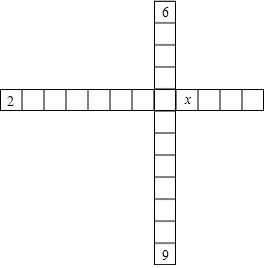 如图,横、竖各12个方格,每个方格都有一个数,已知横行上任意三个相邻数之和为10,竖列上任意三个相邻数之和为18,图中已填入2,6,9和x四个数,那么x代表的数是5.
如图,横、竖各12个方格,每个方格都有一个数,已知横行上任意三个相邻数之和为10,竖列上任意三个相邻数之和为18,图中已填入2,6,9和x四个数,那么x代表的数是5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列说法正确的是( )
如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列说法正确的是( )| A. | AD垂直FE | B. | AD平分EF | C. | EF垂直平分AD | D. | AD垂直平分EF |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com