
【题目】∠AOB内部有一点P,∠AOB=60°.
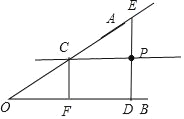
(1)过点P画PC∥OB,交OA于点C;
(2)过点P画PD⊥OB,交OB于点D,交OA于点E;
(3)过点C画直线OB的垂线段CF;
(4)根据所画图形,∠ACF= 度,∠OED= 度.
【答案】(1)见解析;(2)见解析;(3)见解析;(4)150,30..
【解析】
(1)、(2)、(3)利用题中几何语言画出对应的几何图形;
(4)先根据垂直定义得到∠OFC=90°,再利用三角形外角性质可得到∠ACF的度数,再根据平行线的判定方法得到CF∥DE,然后根据两直线平行,同旁内角互补计算∠OED的度数.
解:(1)如图,点C为所作;
(2)如图,点D、E为所作;
(3)如图,CF为所作;
(4)∵CF⊥OB,
∴∠OFC=90°,
∴∠ACF=∠O+∠CFO=60°+90°=150°,
∵DE⊥OB,CF⊥OB,
∴CF∥DE,
∴∠ACF+∠OED=180°,
∠OED=180°﹣150°=30°.
故答案为:150,30.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了配合“八荣八耻”宣传教育,针对闯红灯的现象时有发生的实际情况,八年级某班开展一次题为“红灯与绿灯”的课题学习活动,它们将全班学生分成8个小组,其中第①~⑥组分别负责早.中.晚三个时段闯红灯违章现象的调查,第⑦小组负责查阅有关红绿灯的交通法规,第⑧小组负责收集有关的交通标志. 数据汇总如下:
部分时段车流量情况调查表
时间 | 负责组别 | 车流总量 | 每分钟车流量 |
早晨上学6:30~7:00 | ①② | 2747 | 92 |
中午放学11:20~11:50 | ③④ | 1449 | 48 |
下午放学5:00~5:30 | ⑤⑥ | 3669 | 122 |
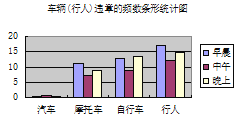
回答下列问题:
(1)请你写出2条交通法规.
(2)早晨.中午.晚上三个时段每分钟车流量的极差是多少,这三个时段的车流总量的中位数是多少.
(3)观察表中的数据及条形统计图,写出你发现的一个现象并分析其产生的原因.
(4)通过分析写一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向点B以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动;如果同时出发,则过3秒时,求△BPQ的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
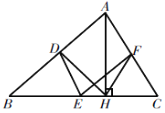
【题目】如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)试判断线段DE与FH之间的数量关系,并说明理由;
(2)求证:∠DHF=∠DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗洪抢险中,解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民,早晨从![]() 地出发,晚上到达
地出发,晚上到达![]() 地,约定向东为正方向,当天的航行路程记录如下(单位:千米):
地,约定向东为正方向,当天的航行路程记录如下(单位:千米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)请你帮忙确定![]() 地位于
地位于![]() 地的什么方向,距离
地的什么方向,距离![]() 地多少千米?
地多少千米?
(2)若冲锋舟每千米耗油![]() 升,邮箱容量为
升,邮箱容量为![]() 升,求冲锋舟当天救灾过程中至少还需补充多少升油?
升,求冲锋舟当天救灾过程中至少还需补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD为矩形,G是BC上的任意一点,DE⊥AG于点E.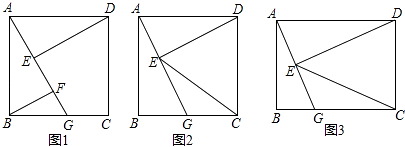
(1)如图1,若AB=BC,BF∥DE,且交AG于点F,求证:AF﹣BF=EF;
(2)如图2,在(1)条件下,AG= ![]() BG,求
BG,求 ![]() ;
;
(3)如图3,连EC,若CG=CD,DE=2,GE=1,则CE=(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的有理数为![]() ,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度由
,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度由![]() 运动,同时,点Q从点B出发以每秒1个单位长度的速度由
运动,同时,点Q从点B出发以每秒1个单位长度的速度由![]() 运动,当点Q到达点A时P、Q两点停止运动,设运动时间为
运动,当点Q到达点A时P、Q两点停止运动,设运动时间为![]() 单位:秒
单位:秒![]() .
.
(1)求![]() 时,求点P和点Q表示的有理数;
时,求点P和点Q表示的有理数;
(2)求点P与点Q第一次重合时的t值;
(3)当t的值为多少时,点P表示的有理数与点Q表示的有理数距离是3个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读并回答:
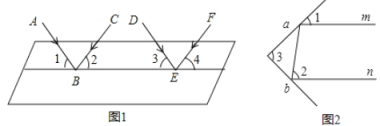
科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.如图1,一束平行光线![]() 与
与![]() 射向一个水平镜面后被反射,此时
射向一个水平镜面后被反射,此时![]() ,
,![]() .
.
①由条件可知:![]() 与
与![]() 的大小关系是____________,理由是____________;
的大小关系是____________,理由是____________;![]() 与
与![]() 的大小关系是____________;
的大小关系是____________;
②反射光线![]() 与
与![]() 的位置关系是____________,理由是____________;
的位置关系是____________,理由是____________;
(2)解决问题:
如图2,,一束光线![]() 射到平面镜
射到平面镜![]() 上,被
上,被![]() 反射到平面镜
反射到平面镜![]() 上,又被
上,又被![]() 镜反射,若
镜反射,若![]() 反射出的光线
反射出的光线![]() 平行于
平行于![]() ,且
,且![]() ,求
,求![]() 和
和![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com