
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于
点O,线段OA,OB的中点分别为E,F。 (1)求证:△FOE≌△DOC;
(2)求tan∠BOC的值; (3)设△AGE, △EFO,△BFH的面积分别为S1,S2, S3,
求S1: S2: S3 的值。
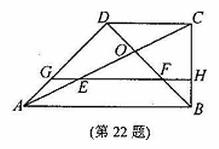
(1)证明:∵EF是△OAB的中位线,
∴EF∥AB,EF=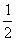 AB,
AB,
 而CD∥AB,CD=
而CD∥AB,CD=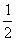 AB,
AB,
∴EF=CD,∠OEF=∠OCD,∠OFE=∠ODC,
∴△FOE≌△DOC;(4分)
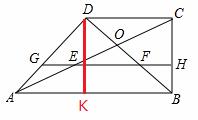
(2) 过点D作DK⊥AB,DK=BC ,BK=DC=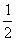 AB=AK,
AB=AK,
∴∠DAB=45°而CD∥AB,∴∠ADC=135°
∵BC=CD, ∠BCD=90°
∴∠DCB=45°
∴∠ADO=90°
∵CD∥AB,∴△DOC∽△BOA
∴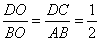 ,设DO=a,则AD=BO=3a
,设DO=a,则AD=BO=3a
∴tan∠BOC=tan∠AOD=3(4分)
(3) ∵ EF∥AB∥CD
∴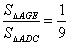 ,
,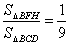 ,而
,而 ∴
∴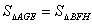
∵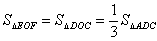 ∴S1: S2: S3= 1:3:1(4分)
∴S1: S2: S3= 1:3:1(4分)


科目:初中数学 来源: 题型:
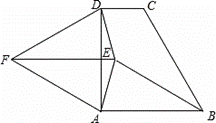
如图,直角梯形ABCD,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边△ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(1)求证:EB=EF;
(2)四边形ABEF是哪一种特殊四边形?(直接写出特殊四边形名称)
(2)若EF=6,求直角梯形ABCD的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q.
当CQ=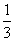 CE时,EP+BP= ;
CE时,EP+BP= ;
当CQ=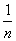 CE时,EP+BP=
CE时,EP+BP=

查看答案和解析>>
科目:初中数学 来源: 题型:
彼此相似的矩形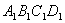 ,
,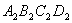 ,
,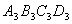 ,…,按如图所示的方式放置.点
,…,按如图所示的方式放置.点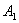 ,
,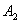 ,
,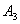 ,…,和点
,…,和点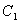 ,
,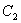 ,
,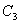 ,…,分别在直线
,…,分别在直线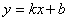 (k>0)和x轴上,已知点
(k>0)和x轴上,已知点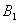 、
、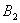 的坐标分别为(1,2),(3,4),则Bn的坐标是( )
的坐标分别为(1,2),(3,4),则Bn的坐标是( )
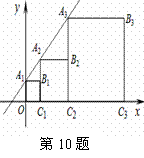 |
A.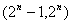 B.
B.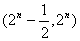 C.
C.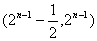 D.
D. 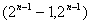
查看答案和解析>>
科目:初中数学 来源: 题型:
材料:① 1的任何次幂都为1;② -1的奇数次幂为-1;③ -1的偶数次幂也为1;④任何不等于零的数的零次幂都为1;请问当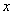 为何值时,代数式
为何值时,代数式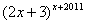 的值为1.
的值为1.
查看答案和解析>>
科目:初中数学 来源: 题型:
若将函数y=3x2的图象向右平行移动1个单位,再向上平移5个单位,可得到的抛物线是
A.y=3(x+1)2-5 B.y=3(x+1)2+5 C.y=3(x-1)2-5 D.y=3(x-1)2+5
查看答案和解析>>
科目:初中数学 来源: 题型:
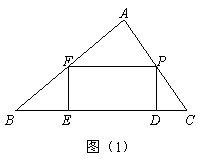
如图①,P是△ABC边AC上的动点,以P为顶点作矩形PDEF,顶点D,E在边BC上,顶点F在边AB上;△ABC的底边BC及BC上的高的长分别为a,h,且是关于x的一元二次方程mx 2+nx+k=0的两个实数根,设过D, E,F三点的⊙O的面积为S⊙O,矩形PDEF的面积为S矩形PDEF.
E,F三点的⊙O的面积为S⊙O,矩形PDEF的面积为S矩形PDEF.
(1)求证:以a+h为边长的正方形面积与以a,h为边长的矩形面积之比不小于4;
(2)求 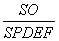 的最小值;
的最小值;
 (3) 当
(3) 当 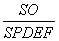 的值最小时,过点A作BC的平行线交直线BP于Q,这时线段AQ的长与m,n,k的取值是否有关?请说明理由.
的值最小时,过点A作BC的平行线交直线BP于Q,这时线段AQ的长与m,n,k的取值是否有关?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com