
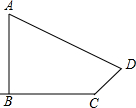
 如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=12m,斜坡坡面上的影长CD=4m,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.(结果保留一位小数,参考数据:$\sqrt{3}$≈1.732).
如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=12m,斜坡坡面上的影长CD=4m,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.(结果保留一位小数,参考数据:$\sqrt{3}$≈1.732). 分析 AD与BC的延长线交于点E,作DH⊥BC于H,如图,利用含30度的直角三角形三边的关系,在Rt△CDH中计算出DH=$\frac{1}{2}$CD=2,CH=$\sqrt{3}$DH=2$\sqrt{3}$,在Rt△DEH中计算出HE=$\sqrt{3}$DH=2$\sqrt{3}$,则BE=BC+CH+EH=12+4$\sqrt{3}$,然后在Rt△ABE中利用含30度的直角三角形三边的关系求AB的长.
解答 解:AD与BC的延长线交于点E,作DH⊥BC于H,如图,∠DCH=30°,∠DEH=30°,
在Rt△CDH中,∵∠DCH=30°,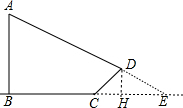
∴DH=$\frac{1}{2}$CD=2,CH=$\sqrt{3}$DH=2$\sqrt{3}$,
在Rt△DEH中,∵∠DEH=30°,
∴HE=$\sqrt{3}$DH=2$\sqrt{3}$,
∴BE=BC+CH+EH=12+4$\sqrt{3}$,
在Rt△ABE中,∵∠AEB=30°,
∴AB=$\frac{\sqrt{3}}{3}$BE=$\frac{\sqrt{3}}{3}$(12+4$\sqrt{3}$)=4$\sqrt{3}$+4≈10.9(m).
答:旗杆AB的高度约为10.9m.
点评 本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.熟练掌握含30度的直角三角形三边的关系是解决此题的关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
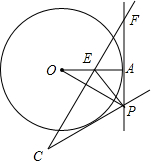 如图,P是⊙O的切线FA上的点,点A为切点,连接OP,OP的垂直平分线FE交OA于点E,连接EP,过点P作PC⊥EP
如图,P是⊙O的切线FA上的点,点A为切点,连接OP,OP的垂直平分线FE交OA于点E,连接EP,过点P作PC⊥EP查看答案和解析>>
科目:初中数学 来源: 题型:选择题
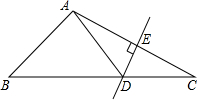 如图所示,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为13cm,则△ABC的周长为( )
如图所示,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为13cm,则△ABC的周长为( )| A. | 16cm | B. | 19cm | C. | 21cm | D. | 25cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,某居民小区的A,B两楼之间的距离MN=30m,两楼高都是20m,A楼在B楼正南,B楼一楼朝南的窗台离地面的距离CN=2m,窗户高1.8m,正午时刻太阳光线与地面成30°角,A楼的影子是否影响B楼一楼窗户采光?若影响,挡住窗户多高?若不影响,请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
如图所示,某居民小区的A,B两楼之间的距离MN=30m,两楼高都是20m,A楼在B楼正南,B楼一楼朝南的窗台离地面的距离CN=2m,窗户高1.8m,正午时刻太阳光线与地面成30°角,A楼的影子是否影响B楼一楼窗户采光?若影响,挡住窗户多高?若不影响,请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com