
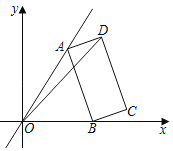
【题目】如图,在平面直角坐标系中,点A在一次函数y=![]() x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2
x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2![]() ,AD=1,则OD的最大值是( )
,AD=1,则OD的最大值是( )
A.![]() B.
B.![]() +2C.
+2C.![]() +2D.
+2D.![]()
【答案】B
【解析】
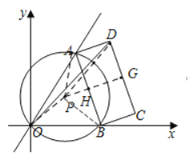
作△AOB的外接圆⊙P,连接OP、PA、PB、PD,作PG⊥CD,交AB于H,垂足为G,易得∠APH=∠AOB,解直角三角形求得PH=2,然后根据三角形三边关系得出OD取最大值时,OD=OP+PD,据此即可求得.
解:∵点A在一次函数y=![]() x图象上,∴tan∠AOB=
x图象上,∴tan∠AOB=![]() ,
,
作△AOB的外接圆⊙P,连接OP、PA、PB、PD,作PG⊥CD,交AB于H,垂足为G,
∵四边形ABCD是矩形,
∴AB∥CD,四边形AHGD是矩形,
∴PG⊥AB,GH=AD=1,
∵∠APB=2∠AOB,∠APH=![]() ∠APB,AH=
∠APB,AH=![]() AB=
AB=![]() =DG,
=DG,
∴∠APH=∠AOB,
∴tan∠APH=tan∠AOB=![]() ,
,
∴![]() =
=![]() ,
,
∴PH=1,
∴PG=PH+HG=1+1=2,
∴PD=![]() =
=![]() =
=![]() ,
,
∴OP=PA=![]() =
=![]() =2,
=2,
在△OPD中,OP+PD≥OD,
∴OD的最大值为:OP+PD=2+![]() ,
,
故选:B.


科目:初中数学 来源: 题型:
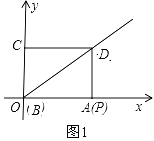
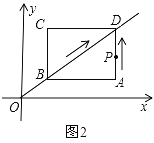
【题目】如图,![]() ,矩形
,矩形![]() 的边
的边![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,
,![]() ,矩形
,矩形![]() 沿射线
沿射线![]() 方向,以每秒1个单位长度的速度运动.同时点
方向,以每秒1个单位长度的速度运动.同时点![]() 从点
从点![]() 出发沿折线
出发沿折线![]() 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点![]() 运动,当点
运动,当点![]() 到达点
到达点![]() 时,矩形
时,矩形![]() 也停止运动,设点
也停止运动,设点![]() 的运动时间为
的运动时间为![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)分别写出点![]() 到
到![]() 、
、![]() 的距离(用含
的距离(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 不与矩形
不与矩形![]() 的顶点重合时,求
的顶点重合时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)设点![]() 到
到![]() 的距离为
的距离为![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
(4)若在点![]() 出发的同时,点
出发的同时,点![]() 从点
从点![]() 以每秒
以每秒![]() 个单位长度的速度向终点A运动,当点
个单位长度的速度向终点A运动,当点![]() 停止运动时,点
停止运动时,点![]() 与矩形
与矩形![]() 也停止运动,设点
也停止运动,设点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,当
,当![]() 的一边与
的一边与![]() 的一边平行时,直接写出线段
的一边平行时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
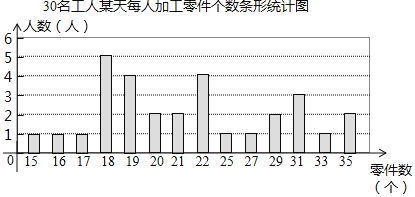
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点D是
,点D是![]() 边的中点,点P是边
边的中点,点P是边![]() 上的一个动点,过点P作射线
上的一个动点,过点P作射线![]() 的垂线,垂足为点E,连接
的垂线,垂足为点E,连接![]() .设
.设![]() ,
,![]() .小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
.小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
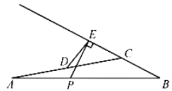
(1)通过取点、画图、测量,得到了x与y的几组值,如表:
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.4 |
y/cm | 1.6 | 1.3 | 1.0 | 0.9 | 1.0 | 1.3 | 2.1 | 2.5 | 2.9 |
(说明:补全表格时相关数据保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:点E是![]() 边的中点时,
边的中点时,![]() 的长度约为________cm.
的长度约为________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:
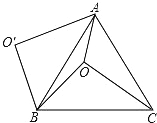
①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;
②连接OO′,则OO′=4;
③∠AOB=150°;
④S四边形AOBO′=6+4![]() .
.
其中正确的结论是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
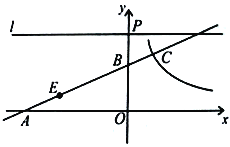
【题目】已知:如图,直线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,线段
,线段![]() 的长是方程
的长是方程![]() 的一个根,请解答下列问题:
的一个根,请解答下列问题:
(1)求点![]() 的坐标;
的坐标;
(2)双曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,点![]() 在线段
在线段![]() 上,
上,![]() ,直线
,直线![]() 轴,垂足为
轴,垂足为![]() ,点
,点![]() 在直线
在直线![]() 上,在直线
上,在直线![]() 上的坐标平面内是否存在点
上的坐标平面内是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形?若存在,请求出点
为顶点的四边形是矩形?若存在,请求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=mx2+4x+2.
(1)若函数图象与x轴只有一个交点,求m的值;
(2)是否存在整数m,使函数图象与x轴有两个交点,且两交点横坐标差的平方等于8?若存在,求出符合条件的m值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,点M,N在同一个正比例函数图象上的是( )
A.M(2,﹣3),N(﹣4,6)B.M(﹣2,3),N(4,6)
C.M(﹣2,﹣3),N(4,﹣6)D.M(2,3),N(﹣4,6)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com