
分析 (1)利用数轴的特点和函数y=|x-1|+|x-3|的最小值的几何意义即可;
(2)借助(1)的结论即可得出x=2时,求出y的最小值即可;
(3)借助(1)(2)结论分n为偶数和奇数分类讨论求出即可,
(4)借助(3)的结论,类比出结论,即可求出.
解答 解:(1)函数y=|x-1|+|x-3|的最小值的几何意义是数轴上x到1和3两点距离之和的最小值,
∵两点之间线段最短,
∴当1<x<3时,ymin=|3-1|=2,
(2)∵y=|x-1|+|x-2|+|x-3|=(|x-1|+|x-3|)+|x-2|,
当x=2时,|x-2|有最小值,
∴结合(1)的结论得出,当x=2时,ymin=2+0=2,
(3)当n为偶数时,y=|x-1|+|x-2|+…+|x-n|=(|x-1|+|x-n|)+(|x-2|+|x-(n-1)|)+…+(|x-$\frac{n}{2}$|+|x-($\frac{n}{2}$+1)|),
由(1)知,当$\frac{n}{2}$<x<$\frac{n}{2}$+1时,
|x-1|+|x-n|有最小值n-1,
|x-2|+|x-(n-1)|有最小值(n-1)-2=n-3,
…
|x-$\frac{n}{2}$|+|x-($\frac{n}{2}$+1)|有最小值1,
∴当$\frac{n}{2}$<x<$\frac{n}{2}$+1时,
ymin=1+3+5+…+(n-3)+(n-1)=$\frac{{n}^{2}}{4}$,
当n为奇数时,y=|x-1|+|x-2|+…+|x-n|=(|x-1|+|x-n|)+(|x-2|+|x-(n-1)|)+…+(|x-$\frac{n-1}{2}$|+|x-($\frac{n+1}{2}$+1)|)+|x-$\frac{n+1}{2}$|,
由(1)知,当x=$\frac{n+1}{2}$时,
|x-1|+|x-n|有最小值n-1,
|x-2|+|x-(n-1)|有最小值(n-1)-2=n-3,
…
|x-$\frac{n}{2}$|+|x-($\frac{n}{2}$+1)|有最小值1,
|x-$\frac{n+1}{2}$|的最小值为0,
∴当x=$\frac{n+1}{2}$时,ymin=0+2+4+…+(n-3)+(n-1)=$\frac{{n}^{2}-1}{4}$,
(4)类似(3)的做法可知,y=|x-a1|+|x-a2|+…+|x-an|,
如果n为偶数时,当${a}_{\frac{n}{2}}<x<{a}_{\frac{n}{2}+1}$时,y有最小值,
如果n为奇数时,当x=${a}_{\frac{n+1}{2}}$时,y有最小值;
∵y=|x-1|+|2x-1|+…+|8x-1|+|9x-1|
=$\stackrel{9个}{|x-\frac{1}{9}|+…+|x-\frac{1}{9}|}$+$\stackrel{8个}{|x-\frac{1}{8}|+…+|x-\frac{1}{8}|}$+…+$\stackrel{2个}{|x-\frac{1}{2}|+|x-\frac{1}{2}|}$+|x-1|
∴共有9+8+7+…+2+1=45项,为奇数.
∴当x=$\frac{1}{7}$时,ymin=|$\frac{1}{7}$-1|+|$\frac{2}{7}$-1|+…+|$\frac{8}{7}$-1|+|$\frac{9}{7}$-1|=$\frac{24}{7}$
点评 此题是绝对值题目,主要考查了绝对值的几何意义和两个绝对值的和的几何意义,分类讨论思想,解本题的关键是找出规律,运用规律.是一道难度比较大竞赛题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.85a | B. | 0.15a | C. | $\frac{a}{0.15}$ | D. | $\frac{a}{0.85}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
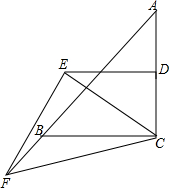 如图,△ABC为等腰Rt△,∠ACB=90°,D为AC中点,F为AB延长线上一点,作DE∥BC,且∠ECF=45°,说明CE、EF的关系.
如图,△ABC为等腰Rt△,∠ACB=90°,D为AC中点,F为AB延长线上一点,作DE∥BC,且∠ECF=45°,说明CE、EF的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,点E是线段AD上的一点,以EC为斜边作等腰直角△ECF,连接BF,若AE=2,DE=3,则线段BF的长度为2$\sqrt{13}$.
如图,在正方形ABCD中,点E是线段AD上的一点,以EC为斜边作等腰直角△ECF,连接BF,若AE=2,DE=3,则线段BF的长度为2$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10的平方根是100 | B. | -2不是4的平方根 | ||
| C. | $\frac{4}{9}$的平方根是$\frac{2}{3}$ | D. | 0.01的算术平方根是0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com