
 如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据:$\sqrt{3}$≈1.732)
如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据:$\sqrt{3}$≈1.732) 分析 根据sin30°=$\frac{CF}{BC}$=$\frac{CF}{30}$,求出CF的长,根据sin60°=$\frac{BG}{AB}$,再求出BF的长,即可得出CE的长.
解答 解:由题意得:AD⊥CE,
过点B作BF⊥CE,BG⊥EA,
∵灯罩BC长为30cm,光线最佳时灯罩BC与水平线所成的角为30°,
∵CF⊥FB,即三角形CFB为直角三角形,
∴sin30°=$\frac{CF}{BC}$=$\frac{CF}{30}$,
∴CF=15cm,
在直角三角形ABG中,sin60°=$\frac{BG}{AB}$,
∴$\frac{\sqrt{3}}{2}$=$\frac{BG}{40}$,
解得:BG=20$\sqrt{3}$,
又∠ADC=∠BFD=∠BGD=90°,
∴四边形BFDG为矩形,
∴FD=BG,
∴CE=CF+FD+DE=CF+BG+ED=15+20$\sqrt{3}$+2≈51.6(cm).
答:此时灯罩顶端C到桌面的高度CE是51.6cm.
点评 此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
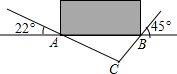 某考古队在一个土坡下发现一个古墓,位置在如图的C点,为了确定古墓C的正确位置,队员小王想出了如下方法:
某考古队在一个土坡下发现一个古墓,位置在如图的C点,为了确定古墓C的正确位置,队员小王想出了如下方法:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
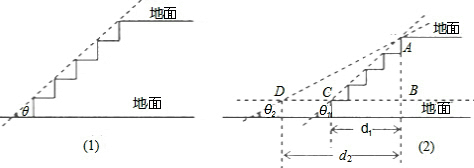
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
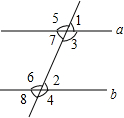 如图,在条件:①∠5=∠6,②∠7=∠2,③∠3+∠8=180°,④∠3=∠2,⑤∠4+∠1=180°中,能判定a∥b的条件有( )
如图,在条件:①∠5=∠6,②∠7=∠2,③∠3+∠8=180°,④∠3=∠2,⑤∠4+∠1=180°中,能判定a∥b的条件有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
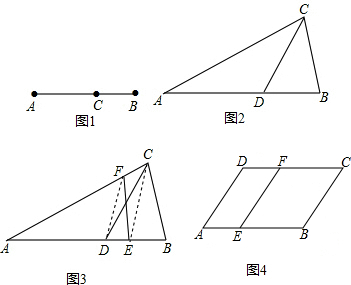
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com