
(1)设△POQ的面积为y,求y关于t的函数解析式;
(2)当△POQ的面积最大时,将△POQ沿直线PQ翻折得到△PCQ,试判断点C是否落在直线AB上,并说明理由.

科目:初中数学 来源: 题型:阅读理解
阅读材料:如图26-①,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部的线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:![]() ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.

解答下列问题:如图26-②,抛物线顶点坐标为点![]() (1,4),交
(1,4),交![]() 轴于点
轴于点![]() (3,0),交
(3,0),交![]() 轴于点
轴于点![]() .
.
(1)求抛物线和直线![]() 的解析式;
的解析式;
(2)求![]() 的铅垂高
的铅垂高![]() 及
及![]() ;
;
(3)设点![]() 是抛物线(在第一象限内)上的一个动点,是否存在一点
是抛物线(在第一象限内)上的一个动点,是否存在一点![]() ,使
,使![]() ,若存在,求出
,若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
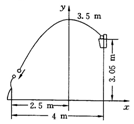
如图26-3-2所示,一位运动员在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,达到最大高度3.5m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式.
(2)该运动员身高1.8m,在这次跳投中,球在头顶上0.25m处出手,问:球出手时,他距离地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
如图26-3-2所示,一位运动员在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,达到最大高度3.5m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式.
(2)该运动员身高1.8m,在这次跳投中,球在头顶上0.25m处出手,问:球出手时,他距离地面的高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知某型汽车在干燥的路面上,汽车停止行驶所需的刹车距离与刹车时的车速之间有下表所示的对应关系.
| 速度v(km/h) | 48 | 64 | 80 | 96 | 112 | … |
| 刹车距离s(m) | 22.5 | 36 | 52.5 | 72 | 94.5 | … |
(1)请你以汽车刹车时的车速为v为自变量,刹车距离s为函数,在如图26-3-7所示的坐标系中描点连线,画出函数的图象;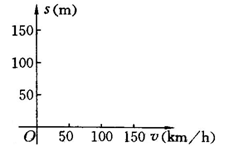
(2)观察所画的函数的图象,你发现了什么?
(3)若把这个函数的图象看成是一条抛物线,请根据表中所给的数据,选择三对,求出它的函数关系式;
(4)用你留下的两对数据,验证一下你所得到的结论是否正确.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com