
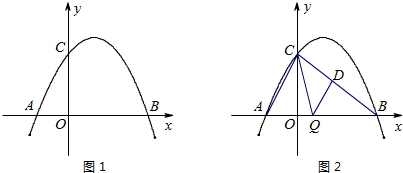
 x2+2x+6�������߶Գ���Ϊx=2����������Ϊ��2��8����(3) P��2��4����(4)2.
x2+2x+6�������߶Գ���Ϊx=2����������Ϊ��2��8����(3) P��2��4����(4)2.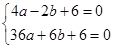 ��
�� ��
�� x2+2x+6��
x2+2x+6�� ��x-2��2+8��
��x-2��2+8��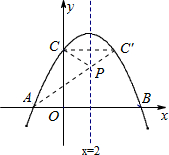
 ��
�� ��
�� AB��OC=24��
AB��OC=24��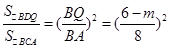
 ��
�� AQ��OC=3m+6��
AQ��OC=3m+6�� -(3m+6)=-
-(3m+6)=- m2+
m2+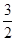 m+
m+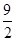 =-
=- ��m-2��2+6��
��m-2��2+6��

 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
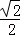 ʱ�����E�����ꣻ
ʱ�����E�����ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
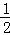 x2+mx+n��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A����1��0����C��0��2����
x2+mx+n��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A����1��0����C��0��2����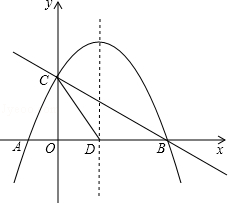
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
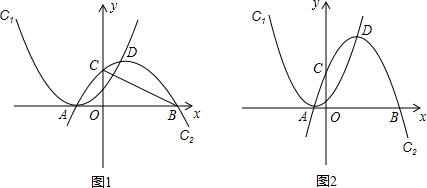
 ��
�� ��m��0��m��
��m��0��m�� ��ʱ����ֱ��д������ABD����������ֱ�ߵľ�����ȵ����е�����꣨�ú�m��ʽ�ӱ�ʾ����
��ʱ����ֱ��д������ABD����������ֱ�ߵľ�����ȵ����е�����꣨�ú�m��ʽ�ӱ�ʾ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
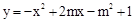 ��x�ύ��ΪA��B����B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C��
��x�ύ��ΪA��B����B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C��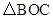 �ǵ��������Σ��������ߵĽ���ʽ��
�ǵ��������Σ��������ߵĽ���ʽ��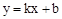 ����P��n��0����x����һ�����㣬�ڣ�2���������£�����P����ֱ��x���ֱ�߽����һ�κ�����ͼ���ڵ�M����������
����P��n��0����x����һ�����㣬�ڣ�2���������£�����P����ֱ��x���ֱ�߽����һ�κ�����ͼ���ڵ�M����������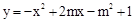 �ڵ�N����ֻ�е�
�ڵ�N����ֻ�е�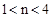 ʱ����Mλ�ڵ�N���·��������һ�κ����Ľ���ʽ��
ʱ����Mλ�ڵ�N���·��������һ�κ����Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
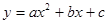 ��ͼ��x����A����1��0����B��2��0������y����C��0����2������A��C��ֱ�ߣ�
��ͼ��x����A����1��0����B��2��0������y����C��0����2������A��C��ֱ�ߣ�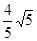 �����M�����꣮
�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
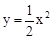 �ϵ�һ�����㣬�ҵ�A�ڵ�һ�����ڣ�AE��y���ڵ�E����B����Ϊ(O��2)��ֱ��AB��
�ϵ�һ�����㣬�ҵ�A�ڵ�һ�����ڣ�AE��y���ڵ�E����B����Ϊ(O��2)��ֱ��AB��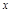 ���ڵ�C����D���C����y��Գƣ�ֱ��DE��AB�ཻ�ڵ�F������BD�����߶�AE�ij�Ϊm����BED�����ΪS��
���ڵ�C����D���C����y��Գƣ�ֱ��DE��AB�ཻ�ڵ�F������BD�����߶�AE�ij�Ϊm����BED�����ΪS��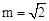 ʱ����S��ֵ��
ʱ����S��ֵ��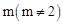 �ĺ�������ʽ��
�ĺ�������ʽ��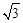 ʱ����
ʱ����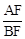 ��ֵ��
��ֵ��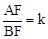 ������k��m��������ϵ��֤����
������k��m��������ϵ��֤����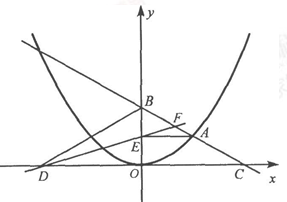
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com