已知k为整数,若关于x的二次方程kx2+(2k+3)x+l=O有有理根,则k的值是 .
【答案】
分析:先根据原方程有有理根可得出此方程的判别式为完全平方数即=(2k+3)
2-4k为完全平方数,设(2k+3)
2-4k=m
2(m为正整数),即4k
2+8k+9-m
2=0,再把此式看作关于k的二次方程,由题设可知此方程有整数根,再根据此方程的判别式为完全平方数即可得到关于n、m的方程组,求出m、n的值,进而可求出k的值.
解答:解:∵关于x的二次方程kx
2+(2k+3)x+l=O有有理根,
∴△
1=(2k+3)
2-4k为完全平方数,
设(2k+3)
2-4k=m
2(m为正整数),即4k
2+8k+9-m
2=0①,
将①式看作关于k的二次方程,由题设可知此方程有整数根,故①式的判别式△
2=64-(9-m
2)=16(m
2-5)应为完全平方数,
令m
2-5=n
2(n为正整数,且m>n),则有(m+n)(m-n)=5,
∴
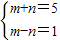
,解得
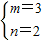
,
将m=2代入①式得k=-2或k=0(舍去),
∴k=-2.
故答案为:-2.
点评:本题考查的是一元二次方程的整数根与有理根,解答此题的关键是熟知若方程有有理根,则此方程的判别式必为完全平方数这一关键知识点.

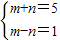 ,解得
,解得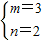 ,
,

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 已知:抛物线y=(k-1)x2+2kx+k-2与x轴有两个不同的交点.
已知:抛物线y=(k-1)x2+2kx+k-2与x轴有两个不同的交点.