
 如图,荆州古城河在CC′处直角转弯,河宽均为5米,从A处到达B处,须经两座桥:DD′,EE′(桥宽不计),设护城河以及两座桥都是东西、南北方向的,A、B在东西方向上相距65米,南北方向上相距85米,恰当地架桥可使ADD′E′EB的路程最短,这个最短路程是多少米?
如图,荆州古城河在CC′处直角转弯,河宽均为5米,从A处到达B处,须经两座桥:DD′,EE′(桥宽不计),设护城河以及两座桥都是东西、南北方向的,A、B在东西方向上相距65米,南北方向上相距85米,恰当地架桥可使ADD′E′EB的路程最短,这个最短路程是多少米?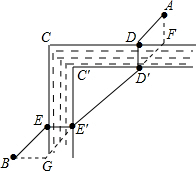
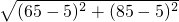 +5×2=110米.
+5×2=110米.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com