
分析 本题对函数的类型不确定,所以要分m=0和m≠0两种情况讨论,当m=0时,为一次函数;当m≠0时,根据题意得出一元二次方程的判别式△=0,得出含m的方程,解方程即可求出m的值.
解答 解:①当m=0时,
y=-2x,为正比例函数,与x轴只有一个交点,满足题意;
②当m≠0时,
根据题意得:y=0时,mx2-2x+mx+$\frac{1}{4}$=0,△=0,
∴(m-2)2-4×$\frac{1}{4}$m=0,
整理得:m2-5m+4=0,
解得:m=1或4,
综上可知满足条件的m值为1、4、0.
故答案为:1、4、0.
点评 本题考查了抛物线与x轴的交点的性质、方程的解法;熟练掌握抛物线与x轴只有一个交点时判别式=0是解决问题的关键.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:解答题
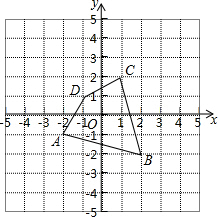 如图,在平面直角坐标系中,O为坐标原点,每个小方格的边长为1个单位长度.四边形ABCD顶点都在格点上,点A的坐标为(-2,-1)
如图,在平面直角坐标系中,O为坐标原点,每个小方格的边长为1个单位长度.四边形ABCD顶点都在格点上,点A的坐标为(-2,-1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
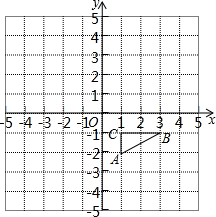 如图所示,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).
如图所示,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
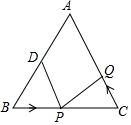 △ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )
△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )| A. | 2 | B. | 5 | C. | 1或5 | D. | 2或3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0)、C(3,0)、D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,以每秒$\frac{1}{2}$个单位的速度沿线段AD向点D运动,运动时间为t秒.过点P作PE⊥x轴交抛物线于点M,交AC于点N.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0)、C(3,0)、D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,以每秒$\frac{1}{2}$个单位的速度沿线段AD向点D运动,运动时间为t秒.过点P作PE⊥x轴交抛物线于点M,交AC于点N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 关于直线对称的两个三角形一定全等 | |
| B. | 两个圆形纸片随意平放在水平桌面上构成轴对称图形 | |
| C. | 若两图形关于直线对称,则对称轴是对应点所连线的垂直平分线 | |
| D. | 等腰三角形一边上的高,中线及这边对角平分线重合 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com