练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    二次函数y＝ax2＋bx＋c的图象如图所示，则一次函数y＝ax＋b与反比例函数y＝在同一平面直角坐标系中的大致图象为

    [　　]

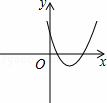
    A．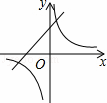

    B．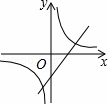

    C．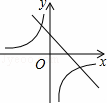

    D．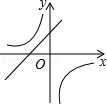

    答案：B
    解析：

    　　分析：根据二次函数图象开口向上得到a＞0，再根据对称轴确定出b，根据与y轴的交点确定出c＞0，然后确定出一次函数图象与反比例函数图象的情况，即可得解．

    　　解答：解：∵二次函数图象开口方向向上，

    　　∴a＞0，

    　　∵对称轴为直线x＝－＞0，

    　　∴b＜0，

    　　∵与y轴的正半轴相交，

    　　∴c＞0，

    　　∴y＝ax＋b的图象经过第一三象限，且与y轴的负半轴相交，

    　　反比例函数y＝图象在第一三象限，

    　　只有B选项图象符合．

    　　故选B．

    　　点评：本题考查了二次函数的图形，一次函数的图象，反比例函数的图象，熟练掌握二次函数的有关性质：开口方向、对称轴、与y轴的交点坐标等确定出a、b、c的情况是解题的关键．


    提示：

    二次函数的图象；一次函数的图象；反比例函数的图象．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

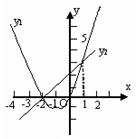
    如图是二次函数y1＝ax2＋bx＋c和一次函数y2＝mx＋n的图象，观察图象写出y2 ≥ y1时，x的取值范围 （   ）
    A．x≥0 B．0≤x≤1C．－2≤x≤1D．x≤-2或x≥1

    查看答案和解析>>

    科目：初中数学 来源：2013-2014学年江苏省无锡市九年级上学期期末考试数学试卷（解析版） 题型：解答题

    如图,已知二次函数y＝ax2＋bx＋c的图象的顶点为M（2,1）,且过点N（3,2）．

    （1）求这个二次函数的关系式;

    （2）若一次函数y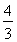＝－x－4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D．设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值？最小值为多少？

     

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年山东省济宁地区九年级第一学期期末考试数学试卷（解析版） 题型：选择题

    抛物线y＝ax2＋bx＋c的顶点坐标是（－1，3），且过点（0，5），那么二次函数y＝ax2＋bx＋c的解析式为

    A．y＝－2x2＋4x＋5                       B．y＝2x2＋4x＋5

    C．y＝－2x2＋4x－1                       D．y＝2x2＋4x＋3

     

    查看答案和解析>>

    科目：初中数学 来源：2012届江苏省昆山市初三第一学期教学调研测试数学卷 题型：选择题

    如图示是二次函数y＝ax2＋bx＋c(a≠0)图象的一部分，图象

       经过A(3，0)，二次函数图象对称轴为x＝l，给出四个结论：

       ①b2>4ac ②bc<0 ③2a＋b＝0 ④a＋b＋c＝0．

       其中正确的是

       A．②④                  B．①③

       C．②③                  D．①④

     

     

    查看答案和解析>>

    科目：初中数学 来源：2012届江苏省姜堰市初二下学期期中考试数学卷 题型：选择题

    已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，给出以下结论：

    ①a＞0．

    ②该函数的图象关于直线对称．

    ③当时，函数y的值都等于0．

    其中正确结论的个数是

     A．3          B．2              C．1              D．0

     

    查看答案和解析>>

    同步练习册答案