
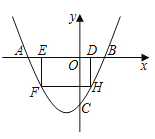
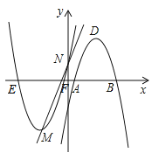
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+(4aЉ1)xЉ4гыxжсНЛгкЕуAЁЂBЃЌгыyжсНЛгкЕуCЃЌЧвOC=2OBЃЌЕуDЮЊЯпЖЮOBЩЯвЛЖЏЕу(ВЛгыЕуBжиКЯ)ЃЌЙ§ЕуDзїОиаЮDEFHЃЌЕуHЁЂFдкХзЮяЯпЩЯЃЌЕуEдкxжсЩЯЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБОиаЮDEFHЕФжмГЄзюДѓЪБЃЌЧѓОиаЮDEFHЕФУцЛ§ЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌОиаЮDEFHВЛЖЏЃЌНЋХзЮяЯпбизХxжсЯђзѓЦНвЦmИіЕЅЮЛЃЌХзЮяЯпгыОиаЮDEFHЕФБпНЛгкЕуMЁЂNЃЌСЌНгMЁЂNЃЎШєMNЧЁКУЦНЗжОиаЮDEFHЕФУцЛ§ЃЌЧѓmЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=![]() x2+xЉ4ЃЛЃЈ2ЃЉ10ЃЛЃЈ3ЃЉmЕФжЕЮЊ
x2+xЉ4ЃЛЃЈ2ЃЉ10ЃЛЃЈ3ЃЉmЕФжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіЕуCЕФзјБъЃЌгЩOCЃН2OBЃЌПЩЭЦГіЕуBзјБъЃЌНЋЕуBзјБъДњШыyЃНax2ЃЋЃЈ4aЉ1ЃЉxЉ4ПЩЧѓГіaЕФжЕЃЌМДПЩаДГіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕуDзјБъЮЊЃЈxЃЌ0ЃЉЃЌгУКЌxЕФДњЪ§ЪНБэЪОГіОиаЮDEFHЕФжмГЄЃЌгУКЏЪ§ЕФЫМЯыЧѓГіШЁЦфзюДѓжЕЪБxЕФжЕЃЌМДЧѓГіЕуDЕФзјБъЃЌНјвЛВНПЩЧѓГіОиаЮDEFHЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМЃЌСЌНгBHЃЌEHЃЌDFЃЌЩшEHгыDFНЛгкЕуGЃЌЙ§ЕуGзїBHЕФЦНааЯпЃЌНЛEDгкMЃЌНЛHFгкЕуNЃЌдђжБЯпMNНЋОиаЮDEFHЕФУцЛ§ЗжГЩЯрЕШЕФСНАыЃЌвРДЮЧѓГіжБЯпBHЃЌMNЕФНтЮіЪНЃЌдйЧѓГіЕуMЕФзјБъЃЌМДПЩЕУГіmЕФжЕЃЎ
НтЃКЃЈ1ЃЉдкХзЮяЯпyЃНax2ЃЋ(4aЉ1)xЉ4жаЃЌ
ЕБxЃН0ЪБЃЌyЃНЉ4ЃЌ
ЁрC(0ЃЌЉ4)ЃЌ
ЁрOCЃН4ЃЎ
ЁпOCЃН2OBЃЌ
ЁрOBЃН2ЃЌ
ЁрB(2ЃЌ0)ЃЌ
НЋB(2ЃЌ0)ДњШыyЃНax2ЃЋ(4aЉ1)xЉ4ЃЌЕУЃКaЃН![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃН![]() x2ЃЋxЉ4ЃЛ
x2ЃЋxЉ4ЃЛ
ЃЈ2ЃЉЩшЕуDзјБъЮЊ(xЃЌ0)ЃЎ
ЁпЫФБпаЮDEFHЮЊОиаЮЃЌ
ЁрH(xЃЌ![]() x2ЃЋxЉ4)ЃЎ
x2ЃЋxЉ4)ЃЎ
ЁпyЃН![]() x2ЃЋxЉ4ЃН
x2ЃЋxЉ4ЃН![]() (xЃЋ1)2Љ
(xЃЋ1)2Љ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЖдГЦжсЮЊxЃНЉ1ЃЌ
ЁрЕуHЕНЖдГЦжсЕФОрРыЮЊxЃЋ1ЃЌ
гЩЖдГЦадПЩжЊDEЃНFHЃН2xЃЋ2ЃЌ
ЁрОиаЮDEFHЕФжмГЄCЃН2(2xЃЋ2)ЃЋ2(Љ![]() x2ЉxЃЋ4)ЃНЉx2ЃЋ2xЃЋ12ЃНЉ(xЉ1)2ЃЋ13ЃЌ
x2ЉxЃЋ4)ЃНЉx2ЃЋ2xЃЋ12ЃНЉ(xЉ1)2ЃЋ13ЃЌ
ЁрЕБxЃН1ЪБЃЌОиаЮDEFHжмГЄШЁзюДѓжЕ13ЃЌ
ЁрДЫЪБH(1ЃЌЉ![]() )ЃЌ
)ЃЌ
ЁрHFЃН2xЃЋ2ЃН4ЃЌDHЃН![]() ЃЌ
ЃЌ
ЁрSОиаЮDEFHЃНHFDH![]() ЃН10ЃЛ
ЃН10ЃЛ
ЃЈ3ЃЉШчЭМЃЌ
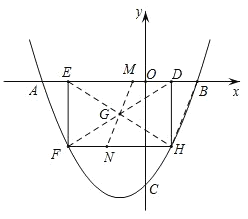
СЌНгBHЃЌEHЃЌDFЃЌЩшEHгыDFНЛгкЕуGЃЌ
Й§ЕуGзїBHЕФЦНааЯпЃЌНЛEDгкMЃЌНЛHFгкЕуNЃЌдђжБЯпMNНЋОиаЮDEFHЕФУцЛ§ЗжГЩЯрЕШЕФСНАыЃЌ
гЩЃЈ2ЃЉжЊЃЌХзЮяЯпЖдГЦжсЮЊxЃНЉ1ЃЌH(1ЃЌЉ![]() )ЃЌ
)ЃЌ
ЁрG(Љ1ЃЌЉ![]() )ЃЌ
)ЃЌ
ЩшжБЯпBHЕФНтЮіЪНЮЊyЃНkxЃЋbЃЌ
НЋЕуB(2ЃЌ0)ЃЌH(1ЃЌЉ![]() )ДњШыЃЌ
)ДњШыЃЌ
ЕУЃК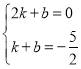 ЃЌНтЕУЃК
ЃЌНтЕУЃК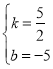 ЃЌ
ЃЌ
ЁржБЯпBHЕФНтЮіЪНЮЊyЃН![]() xЉ5ЃЌ
xЉ5ЃЌ
ЁрПЩЩшжБЯпMNЕФНтЮіЪНЮЊyЃН![]() xЃЋnЃЌ
xЃЋnЃЌ
НЋЕу(Љ1ЃЌЉ![]() )ДњШыЃЌЕУnЃН
)ДњШыЃЌЕУnЃН![]() ЃЌ
ЃЌ
ЁржБЯпMNЕФНтЮіЪНЮЊyЃН![]() xЃЋ
xЃЋ![]() ЃЌ
ЃЌ
ЕБyЃН0ЪБЃЌxЃНЉ![]() ЃЌ
ЃЌ
ЁрM(Љ![]() ЃЌ0)ЃЎ
ЃЌ0)ЃЎ
ЁпB(2ЃЌ0)ЃЌ
ЁрНЋХзЮяЯпбизХxжсЯђзѓЦНвЦ![]() ИіЕЅЮЛЃЌХзЮяЯпгыОиаЮDEFHЕФБпНЛгкЕуMЁЂNЃЌ
ИіЕЅЮЛЃЌХзЮяЯпгыОиаЮDEFHЕФБпНЛгкЕуMЁЂNЃЌ
СЌНгMЁЂNЃЌдђMNЧЁКУЦНЗжОиаЮDEFHЕФУцЛ§ЃЌ
ЁрmЕФжЕЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯп![]() ЃК
ЃК![]() ЕФЖЅЕуЮЊ
ЕФЖЅЕуЮЊ![]() ЃЌгы
ЃЌгы![]() жсЯрНЛгкЕу
жсЯрНЛгкЕу![]() ЃЌЯШНЋХзЮяЯп
ЃЌЯШНЋХзЮяЯп![]() би
би![]() жсЗелЃЌдйЯђгвЦНвЦpИіЕЅЮЛГЄЖШКѓЕУЕНХзЮя
жсЗелЃЌдйЯђгвЦНвЦpИіЕЅЮЛГЄЖШКѓЕУЕНХзЮя![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃЛ
ЃЛ![]() ОЙ§
ОЙ§![]() ЃЌ
ЃЌ![]() СНЕуЃЎ
СНЕуЃЎ
ЃЈ1ЃЉЧѓЕу![]() ЕФзјБъЃЌВЂНсКЯЭМЯѓжБНгаДГіВЛЕШЪНЃК
ЕФзјБъЃЌВЂНсКЯЭМЯѓжБНгаДГіВЛЕШЪНЃК![]() ЕФНтМЏЃЛ
ЕФНтМЏЃЛ
ЃЈ2ЃЉШєХзЮяЯп![]() ЕФЖЅЕу
ЕФЖЅЕу![]() гыЕу
гыЕу![]() ЙигкдЕуЖдГЦЃЌЧѓpЕФжЕМАХзЮяЯп
ЙигкдЕуЖдГЦЃЌЧѓpЕФжЕМАХзЮяЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉШєХзЮяЯп![]() гы
гы![]() жсЕФНЛЕуЮЊ
жсЕФНЛЕуЮЊ![]() ЁЂ
ЁЂ![]() ЃЈЕу
ЃЈЕу![]() ЁЂ
ЁЂ![]() ЗжБ№гыХзЮяЯп
ЗжБ№гыХзЮяЯп![]() ЩЯЕу
ЩЯЕу![]() ЁЂ
ЁЂ![]() ЖдгІЃЉЃЌЪдЮЪЫФБпаЮ
ЖдгІЃЉЃЌЪдЮЪЫФБпаЮ![]() ЪЧКЮжжЬиЪтЫФБпаЮЃПВЂЫЕУїЦфРэгЩЃЎ
ЪЧКЮжжЬиЪтЫФБпаЮЃПВЂЫЕУїЦфРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЬнаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
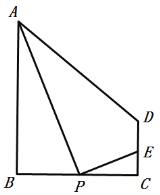
ЃЌ![]() ЃЎPЮЊЯпЖЮ
ЃЎPЮЊЯпЖЮ![]() ЩЯЕФвЛЖЏЕуЃЌЧвКЭBЁЂCВЛжиКЯЃЌСЌНг
ЩЯЕФвЛЖЏЕуЃЌЧвКЭBЁЂCВЛжиКЯЃЌСЌНг![]() ЃЌЙ§ЕуPзї
ЃЌЙ§ЕуPзї![]() НЛЩфЯп
НЛЩфЯп![]() гкЕуEЃЎ
гкЕуEЃЎ
ДЯДЯИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдетИіЮЪЬтНјааСЫбаОПЃК
ЃЈ1ЃЉЭЈЙ§ЭЦРэЃЌЫћЗЂЯж![]() ЃЌЧыФуАяЫћЭъГЩжЄУїЃЎ
ЃЌЧыФуАяЫћЭъГЩжЄУїЃЎ
ЃЈ2ЃЉРћгУМИКЮЛАхЃЌЫћИФБф![]() ЕФГЄЖШЃЌдЫЖЏЕуPЃЌЕУЕНВЛЭЌЮЛжУЪБЃЌ
ЕФГЄЖШЃЌдЫЖЏЕуPЃЌЕУЕНВЛЭЌЮЛжУЪБЃЌ![]() ЁЂ
ЁЂ![]() ЕФГЄЖШЕФЖдгІжЕЃК
ЕФГЄЖШЕФЖдгІжЕЃК
ЕБ![]() ЪБЃЌЕУБэ1ЃК
ЪБЃЌЕУБэ1ЃК
| Ё | 1 | 2 | 3 | 4 | 5 | Ё |
| Ё | 0.83 | 1.33 | 1.50 | 1.33 | 0.83 | Ё |
ЕБ![]() ЪБЃЌЕУБэ2ЃК
ЪБЃЌЕУБэ2ЃК
| Ё | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Ё |
| Ё | 1.17 | 2.00 | 2.50 | 2.67 | 2.50 | 2.00 | 1.17 | Ё |
етЫЕУїЃЌЕуPдкЯпЖЮ![]() ЩЯдЫЖЏЪБЃЌвЊБЃжЄЕуEзмдкЯпЖЮ
ЩЯдЫЖЏЪБЃЌвЊБЃжЄЕуEзмдкЯпЖЮ![]() ЩЯЃЌ
ЩЯЃЌ![]() ЕФГЄЖШгІгавЛЖЈЕФЯожЦЃЎ
ЕФГЄЖШгІгавЛЖЈЕФЯожЦЃЎ
ЂйЬюПеЃКИљОнКЏЪ§ЕФЖЈвхЃЌЮвУЧПЩвдШЗЖЈЃЌдк![]() КЭ
КЭ![]() ЕФГЄЖШетСНИіБфСПжаЃЌ_____ЕФГЄЖШЮЊздБфСПЃЌ_____ЕФГЄЖШЮЊвђБфСПЃЛ
ЕФГЄЖШетСНИіБфСПжаЃЌ_____ЕФГЄЖШЮЊздБфСПЃЌ_____ЕФГЄЖШЮЊвђБфСПЃЛ
ЂкЩш![]() ЃЌЕБЕуPдкЯпЖЮ
ЃЌЕБЕуPдкЯпЖЮ![]() ЩЯдЫЖЏЪБЃЌЕуEзмдкЯпЖЮ
ЩЯдЫЖЏЪБЃЌЕуEзмдкЯпЖЮ![]() ЩЯЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЩЯЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
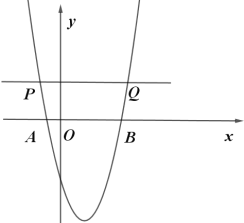
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§yЃНax2ЃЋbxЃ5ЃЈaЃЌbЪЧГЃЪ§ЃЌa![]() 0ЃЉЕФЭМЯѓгыxжсНЛгкЕуAЃЈЃ1ЃЌ0ЃЉКЭЕуBЃЈ5ЃЌ0ЃЉЃЎЖЏжБЯпyЃНtЃЈtЮЊГЃЪ§ЃЉгыХзЮяЯпНЛгкВЛЭЌЕФСНЕуPЁЂQЃЈЕуPдкQЕФзѓВрЃЉЃЎ
0ЃЉЕФЭМЯѓгыxжсНЛгкЕуAЃЈЃ1ЃЌ0ЃЉКЭЕуBЃЈ5ЃЌ0ЃЉЃЎЖЏжБЯпyЃНtЃЈtЮЊГЃЪ§ЃЉгыХзЮяЯпНЛгкВЛЭЌЕФСНЕуPЁЂQЃЈЕуPдкQЕФзѓВрЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЖЏжБЯпyЃНtгыyжсНЛгкЕуCЃЌШєCQ=3CPЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉНЋХзЮяЯпyЃНax2ЃЋbxЃ5дкxжсЯТЗНЕФВПЗжбиxжсЗелЃЌШєЖЏжБЯпyЃНtгыЗелКѓЕФЭМЯёНЛгкЕуMЁЂNЃЌЕуMЁЂNФмЗёЪЧЯпЖЮPQЕФШ§ЕШЗжЕуЃПШєФмЃЌЧѓPQЕФГЄЖШЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
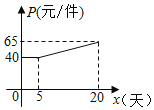
ЁОЬтФПЁПФГЦѓвЕНгЕНвЛХњВњЦЗЕФЩњВњШЮЮёЃЌАДвЊЧѓБиаыдк20ЬьФкЭъГЩЃЌвбжЊУПМўВњЦЗЕФЪлМлЮЊ65дЊЃЌЙЄШЫМзЕкxЬьЩњВњЕФВњЦЗЪ§СПЮЊyМўЃЌyгыxТњзуШчЯТЙиЯЕЃКyЃН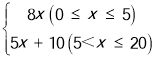 ЃЎ
ЃЎ
ЃЈ1ЃЉЙЄШЫМзЕкМИЬьЩњВњЕФВњЦЗЪ§СПЮЊ100МўЃП
ЃЈ2ЃЉЩшЕкxЬьЃЈ0ЁмxЁм20ЃЉЩњВњЕФВњЦЗГЩБОЮЊPдЊ/МўЃЌPгыxЕФКЏЪ§ЭМЯѓШчЭМЃЌЙЄШЫМзЕкxЬьДДдьЕФРћШѓЮЊWдЊЃЎ
ЂйЧѓPгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкЧѓWгыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіЕкМИЬьЪБЃЌРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
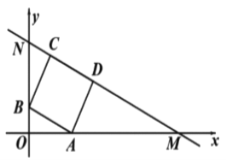
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯп![]() НЛ
НЛ![]() жс,
жс, ![]() жсгкЕу
жсгкЕу![]() ,Еу
,Еу![]() ЪЧ
ЪЧ![]() ЩЯЕФЕуЃЌвд
ЩЯЕФЕуЃЌвд![]() ЮЊБпзїе§ЗНаЮ
ЮЊБпзїе§ЗНаЮ![]() ЧЁКУТфдк
ЧЁКУТфдк![]() ЩЯЃЌвбжЊ
ЩЯЃЌвбжЊ![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЮЊ( )
ЕФжЕЮЊ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁаТНјвЛХњЩЬЦЗЃЌУПИіГЩБОМл25дЊЃЌЯњЪлвЛЖЮЪБМфЗЂЯжЯњЪлСПyЃЈИіЃЉгыЯњЪлЕЅМлxЃЈдЊ/ИіЃЉжЎМфГЩвЛДЮКЏЪ§ЙиЯЕЃЌШчЯТБэЃК

ЃЈ1ЃЉЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєИУЩЬЦЗЕФЯњЪлЕЅМлдк45дЊЁЋ80дЊжЎМфИЁЖЏЃЌ
ЂйЯњЪлЕЅМлЖЈЮЊЖрЩйдЊЪБЃЌЯњЪлРћШѓзюДѓЃПДЫЪБЯњЪлСПЮЊЖрЩйЃП
ЂкЩЬГЁЯывЊдкетЖЮЪБМфФкЛёЕУ4550дЊЕФЯњЪлРћШѓЃЌЯњЪлЕЅМлгІЖЈЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
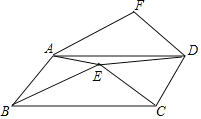
ЁОЬтФПЁПШчЭМЃЌЕуEдкABCDЕФФкВПЃЌAFЁЮBEЃЌDFЁЮCEЃЎ
ЃЈ1ЃЉЧѓжЄ![]() BCEЁе
BCEЁе![]() ADFЃЛ
ADFЃЛ
ЃЈ2ЃЉШєABCDЕФУцЛ§ЮЊ96cm2ЃЌЧѓЫФБпаЮAEDFЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШєХзЮяЯп![]() гыжБЯп
гыжБЯп![]() ЮЇГЩЕФЗтБеЭМаЮФкВПЃЈВЛАќРЈБпНчЃЉга
ЮЇГЩЕФЗтБеЭМаЮФкВПЃЈВЛАќРЈБпНчЃЉга![]() ИіећЕуЃЈКсзнзјБъОљЮЊећЪ§ЃЉЃЌдђвЛДЮКЏЪ§
ИіећЕуЃЈКсзнзјБъОљЮЊећЪ§ЃЉЃЌдђвЛДЮКЏЪ§![]() ЕФЭМЯёЮЊЃЈ ЃЉ
ЕФЭМЯёЮЊЃЈ ЃЉ
A.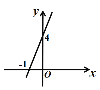
B.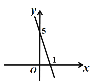
C.
D.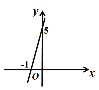
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com