
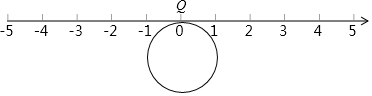
分析 (1)利用圆的半径以及滚动周数即可得出滚动距离;
(2)①Q点回到原点即3次滚动周数的代数和为0;Q点距离原点4π,由于半径为1,即3次滚动周数的代数和为±2;
②利用绝对值得性质以及有理数的加减运算得出移动距离即可.
解答 解:(1)把圆片沿数轴向左滚动1周,点Q到达数轴上点A的位置,点A表示的数是-2π;
故答案为:-2π;
(2)①∵+3-1=2,2-2=0,
∴第3次滚动-2周后,Q点回到原点;
∵+3-1-2+4-3=1,1+1=2或1-3=-2,
∴第6次滚动1或-3周后,Q点距离原点4π
故答案为-2,1或-3;
②根据题意列得:3+1+2+4+3+1=14,14×2π=28π,
或 3+1+2+4+3+3=16,6×2π=32π.
当圆片结束运动时,Q点运动的路程共有28π或32π.
点评 此题主要考查了数轴的应用以及绝对值得性质和圆的周长公式应用,利用数轴得出对应数是解题关键


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
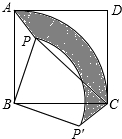 已知:如图,点P是正方形ABCD内一点,连接PA、PB、PC.
已知:如图,点P是正方形ABCD内一点,连接PA、PB、PC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段AB,请按要求完成下列问题.
如图,已知线段AB,请按要求完成下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com