
分析 (1)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(2)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
解答 解:(1)abx2-(a3+b3)x+a2b2=0,
(ax-b2)(bx-a2)=0,
∴ax-b2=0,或bx-a2=0,
∵ab≠0,
∴a≠0,b≠0,
∴x1=$\frac{{b}^{2}}{a}$,x2=$\frac{{a}^{2}}{b}$;
(2)mx2-(m-n)x-n=0,
(mx+1)(x-n)=0.
∴mx+1=0,或x-n=0,
∵m≠0,
∴x1=-$\frac{1}{m}$,x2=n.
点评 此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:选择题
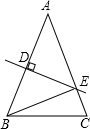 如图,在△ABC中,AC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,EC=2cm,则BE的长为( )
如图,在△ABC中,AC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,EC=2cm,则BE的长为( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个残破的车轮如图所示,测得它所剩圆弧两端点间的距离a=60cm,弧的中点到弧所对的弦的距离h=10cm,如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少?
一个残破的车轮如图所示,测得它所剩圆弧两端点间的距离a=60cm,弧的中点到弧所对的弦的距离h=10cm,如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com