
分析 ①画AB的垂直平分线交x轴于一点;
②以A为圆心,AB长为半径交x轴于两点;
③以B为圆心,AB长为半径交交x轴于一点,再分别写出坐标即可.
解答 解:如图所示: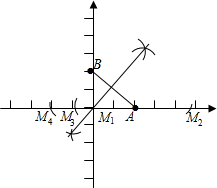
M1(0,0),M4(-2,0),
∵A(2,0),B(0,2),
∴AB=$\sqrt{{2}^{2}+{2}^{2}}=2\sqrt{2}$,
∵M2,M3是以A为圆心,AB长为半径交x轴于两点,
∴M2(2+2$\sqrt{2}$,0),M3(-2$\sqrt{2}$+2,0).
故所有满足条件点M的坐标是:(0,0)(-2,0)(2+2$\sqrt{2}$,0),(-2$\sqrt{2}$+2,0).
点评 此题主要考查了等腰三角形的判定与性质.注意分类讨论与数形结合思想的应用是解此题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 500(1+2x)=700 | B. | 500(1+x2)=700 | C. | 500(1+x)2=700 | D. | 700(1+x2)=500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
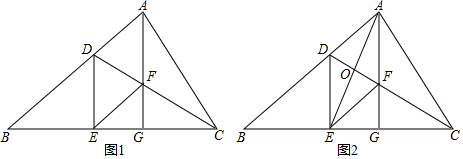
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com