
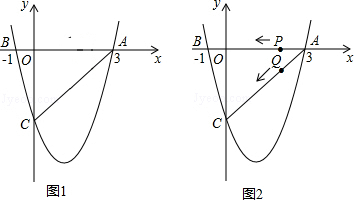
分析 (1)将A,B点坐标代入函数y=ax2+bx-4中,求得b、a,进而可求解析式;
(2)由解析式先求得点D、C坐标,再根据S△ACD=S梯形AOMD-S△CDM-S△AOC,列式计算即可;
(3)注意到P,Q运动速度相同,则△APQ运动时都为等腰三角形,又由A、E对称,则AP=EP,AQ=EQ,易得四边形四边都相等,即菱形.利用菱形对边平行且相等的性质可用t表示E点坐标,又E在二次函数的图象上,所以代入即可求t,进而E可表示.
解答 解:(1)把点A(3,0),B(-1,0)代入y=ax2+bx-4(a≠0)得:
$\left\{\begin{array}{l}{9a+3b-4=0}\\{a-b-4=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{4}{3}}\\{b=-\frac{8}{3}}\end{array}\right.$;
(2)过点D作DM⊥y轴于点M,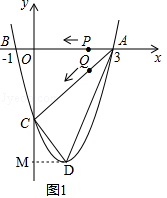
∵y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4=$\frac{4}{3}$(x-1)2-$\frac{16}{3}$,
∴点D(1,-$\frac{16}{3}$)、点C(0,-4),
则S△ACD=S梯形AOMD-S△CDM-S△AOC
=$\frac{1}{2}$×(1+3)×$\frac{16}{3}$-$\frac{1}{2}$×($\frac{16}{3}$-4)×1-$\frac{1}{2}$×3×4
=4;
(3)四边形APEQ为菱形,E点坐标为(-$\frac{5}{8}$,-$\frac{29}{16}$).理由如下
如图2,E点关于PQ与A点对称,过点Q作,QF⊥AP于F,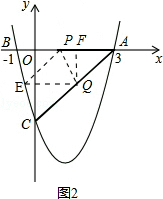
∵AP=AQ=t,AP=EP,AQ=EQ
∴AP=AQ=QE=EP,
∴四边形AQEP为菱形,
∵FQ∥OC,
∴$\frac{AF}{AO}$=$\frac{FQ}{OC}$=$\frac{AQ}{AC}$,
∴$\frac{AF}{3}$=$\frac{FQ}{4}$=$\frac{t}{5}$
∴AF=$\frac{3}{5}$t,FQ=$\frac{4}{5}$t•
∴Q(3-$\frac{3}{5}$t,-$\frac{4}{5}$t),
∵EQ=AP=t,
∴E(3-$\frac{3}{5}$t-t,-$\frac{4}{5}$t),即E(3-$\frac{8}{5}$t,-$\frac{4}{5}$t),
∵E在二次函数y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4上,
∴-$\frac{4}{5}$t=$\frac{4}{3}$(3-$\frac{8}{5}$t)2-$\frac{8}{3}$(3-$\frac{8}{5}$t)-4,
∴t=$\frac{145}{64}$,或t=0(与A重合,舍去),
则3-$\frac{8}{5}$t=-$\frac{5}{8}$,-$\frac{4}{5}$t=-$\frac{29}{16}$,
∴E(-$\frac{5}{8}$,-$\frac{29}{16}$).
点评 本题考查了二次函数性质、利用勾股定理解直角三角形及菱形等知识,总体来说题意复杂但解答内容都很基础,熟练地运用数形结合是解决问题的关键.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
 如图,BD为?ABCD的对角线,按要求完成下列各题.
如图,BD为?ABCD的对角线,按要求完成下列各题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+1=0 | B. | x2+x-1=0 | C. | x2+2x-3=0 | D. | 4x2-4x+1=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com