
����Ŀ��Ϊ�˷ḻѧ��У�������ѧ���Ķ�Ԫ�Ļ����ٽ�ѧ�����Ľ�����г��չ��ѧУ��չ�˷ḻ��ʵ����Ż.����ij��ѧ��չ�����Ż�У�A.�ȿ����B.���衢C.��ë��D.���١�E.ɳ��.ѧ����������Ϊ���˽�ȫУ800��ѧ������������չ��һ�ε����о����뽫����ĵ�����̲�ȫ.
�������飺ѧ���������ļƻ�ѡȡ40��ѧ�������ʾ����飬����ij��������У� �������� ������ţ���
�����ߡ��ˡ��������꼶�������ȡ40��Ů�������ʾ����飻
�����ߡ��ˡ��������꼶�������ȡ�С�Ů����40�������ʾ�����.
�ռ����ݣ���������ȷ����ѧ�����������ռ����������ݣ�������Ŀ�ı�ţ�����ĸ���ű�ʾ��
B��E��B��A��E��C��C��C��B��B
A��C��E��D��B��A��B��E��C��A
D��D��B��B��C��C��A��A��E��B
C��B��D��C��A��C��C��A��C��E
�������������ݣ����ǡ������������������ݡ�����ͳ��ͼ���£��벹ȫͳ�Ʊ���ͳ��ͼ.
ѡ���������Ŀ������ͳ�Ʊ�
������Ŀ | ���� | ���� |
A�ȿ����� | �� | 8 |
B���� | ||
C��� | �����B | 12 |
D���� | ||
Eɳ�� | ��һ | 6 |
�ϼ� | 40 | 40 |

�������ݡ��ƶϽ���:
��1��������ͳ��ͼ�У���B���������ڵ����ε�Բ�Ľǵ��� �ȣ�
��2������ѧ���������Ļ�õ��������ݹ���ȫУ��Լ�ж�����ͬѧѡ����ë��������ţ�
���𰸡��������飺�ڣ��������������ݣ����������������ݡ��ƶϽ��ۣ���1��90������2��240��.
��������
�������飺���ݳ�����������ȡ��������Ҫ�߱����������ɵã�
�������������ݣ������ռ������ݣ�����������������ټ����B��D�İٷֱȿɲ�ȫ����ͳ��ͼ��
�������ݡ��ƶϽ��ۣ���1����360������B����Ӧ�İٷֱȣ���2��������������ѡ����ë���Ӧ�ٷֱȿɵã�
�⣺�������飺�������ǣ��ڴ��ߡ��ˡ��������꼶�������ȡ�С�Ů����40�������ʾ����飮
�ʴ�Ϊ���ڣ�
�������������ݣ���ȫͳ�Ʊ����£�
������Ŀ | ���� | ���� |
A�ȿ����� | �� | 8 |
B���� | ���� | 10 |
C��� | �����B | 12 |
D���� |
| 4 |
Eɳ�� | ��һ | 6 |
�ϼ� | 40 | 40 |
ѡ��B������ռ�İٷֱ�Ϊ��10��40=25%��ѡ��D������ռ�İٷֱ�Ϊ��4��40=10%��
��ȫ����ͳ��ͼ���£�
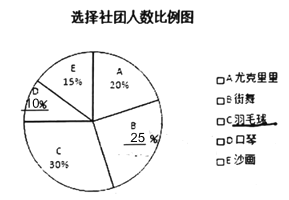
�������ݡ��ƶϽ��ۣ�
��1��������ͳ��ͼ�У���B���������ڵ����ε�Բ�Ľ�Ϊ��360���25%��90����
��2������ȫУѡ����ë�����ŵ�ͬѧ��ԼΪ��800��30%��240��.


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ��ֱ�߹���![]() ������������
������������![]() ����A��B���㣬���е�A�ĺ�������-2.
����A��B���㣬���е�A�ĺ�������-2.
��������ֱ�ߵĺ�����ϵʽ����B������ ��
����![]() �����Ƿ���ڵ�C,ʹ��ABC��ֱ�������Σ������ڣ������C�����꣬�������ڣ���˵�����ɣ�
�����Ƿ���ڵ�C,ʹ��ABC��ֱ�������Σ������ڣ������C�����꣬�������ڣ���˵�����ɣ�
��.���߶�AB��һ��P,��PM��![]() �ᣬ���������ڵ�M,��M�ڵ�һ���ޣ���
�ᣬ���������ڵ�M,��M�ڵ�һ���ޣ���![]() ������M�ĺ�����Ϊ��ֵʱ��MN+3MP�ij���������ֵ�Ƕ��٣�
������M�ĺ�����Ϊ��ֵʱ��MN+3MP�ij���������ֵ�Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��С�����̨�Ϸ�����һ��ɹ�¼ܣ���ͼ2��ɹ�¼ܵIJ���ʾ��ͼ������AB��CD�ཻ�ڵ�O��B��D�������ڵ��棬��������AB=CD=136cm��OA=OC=51cm��OE=OF=34cm���ֽ�ɹ�¼���ȫ�ȹ��ſ�������EF��һ��ֱ�ߣ���EF=32cm��
��1����֤��AC��BD��
��2�������EF������AB�ļн���OEF�Ķ�������ȷ��0.1������
��3��С�������ȹ�����¼ܺ���ܳ��ȴﵽ122cm��������ɹ�¼����Ƿ�����䵽���棿��ͨ������˵�����ɣ�
���ο����ݣ�sin61.9���0.882��cos61.9���0.471��tan61.9���0.553����ʹ�ÿ�ѧ��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����������ˮƽ����Ϊ24 m����A����D��ĸ���Ϊ60�㣬���C�������Ϊ40�㣬��������������ĸߣ�(![]() ��1.732��tan 40���0.8391����ȷ��0.01 m)
��1.732��tan 40���0.8391����ȷ��0.01 m)
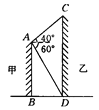
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ָ��С������ҵ(��ͼ)����һ����ʼ���ִ��������������������ȷ�����

(2)��a��b�Dz���ʽ��![]() ��������(a��b)����(1)�з�ʽ��ֵ��
��������(a��b)����(1)�з�ʽ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽����ͼ��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ����
����![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��ֱ��
��ֱ��![]() ������
������![]() �͵�
�͵�![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��
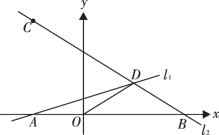
��1����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����֤��![]() �ǵ��������Σ�
�ǵ��������Σ�
��3����![]() �������
�������
��4��̽����ֱ��![]() ���Ƿ�������ڵ�
���Ƿ�������ڵ�![]() ����һ��
����һ��![]() ��ʹ��
��ʹ��![]() ��
��![]() �������ȣ������ڣ���ֱ��д����
�������ȣ������ڣ���ֱ��д����![]() �����ꣻ�������ڣ�˵�����ɣ�
�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b��c���������մ�С�������У��м��������MID{a��b��c}��ֱ��y��kx��2k��k��0���뺯��y��MID{![]() ��2x��1����x��2}��ͼ������ֻ��1�����㣬��k��ȡֵ��Χ��______��
��2x��1����x��2}��ͼ������ֻ��1�����㣬��k��ȡֵ��Χ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+3�ĶԳ�����ֱ��x=1��
��1����֤��2a+b=0��
��2��������x�ķ���ax2+bx��8=0��һ����Ϊ4���̵���һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����ֱ�������Ӧ�ĺ�����
![]() ��
��![]() ��
��![]() ��
��![]() ��
�� ![]() ��
��![]() ��
�� ![]() ��
�� ![]() ����
����
����������________________________________
������ ____________________________________
������ ____________________________________
�Ǹ����� ___________________________________
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com