
解方程:
(1)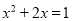 (2)
(2)
科目:初中数学 来源:江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
已知有理数a,b在数轴上对应的点如图所示,则下列各式正确的是( )

A. ab>0 B. |a|>|b| C. a-b>0 D. a+b>0
C 【解析】试题解析:A. 根据b<0,a>0,则ab<0,故A错误; B. 由于b0,故C正确; D. 根据:|a|<|b|,且a>0,b<0,则a+b<0,故D错误. 故选C.查看答案和解析>>
科目:初中数学 来源:甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型:解答题
计算题

查看答案和解析>>
科目:初中数学 来源:甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型:单选题
由3点30分到3点45分,时钟的分针转过的角度是( )
A. 30° B. 45° C. 60° D. 90°
D 【解析】时钟的分针每分钟转过的角度为6°, 所以,由3点30分到3点45分,时钟的分针转过的角度为:6°×(45-30)=90°, 故选D.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型:解答题
如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,∠AOD=∠APC.
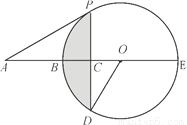
(1)求证:AP是⊙O的切线;
(2)若⊙O的半径是4,AP=4 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型:填空题
已知⊙O半径为1,A、B在⊙O上,且 ,则AB所对的圆周角为__o.
,则AB所对的圆周角为__o.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型:单选题
小明从二次函数 的图象(如图)中观察得到了下面五条信息:①
的图象(如图)中观察得到了下面五条信息:① ; ②
; ② ;③
;③ ;④
;④ ;则其中结论正确的个数是( )
;则其中结论正确的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
A 【解析】试题解析:①因为函数图象与y轴的交点在y轴的负半轴可知,c<0, 由函数图象开口向上可知,a>0,由①知,c<0, 由函数的对称轴在x的正半轴上可知, 故b<0,故abc>0;故此选项正确; ②因为函数的对称轴为故2a=?3b,即2a+3b=0;故此选项错误; ③因为图象和x轴有两个交点,所以,故此选项正确; ④把x=1代入得:a+b+c<0,故此选...查看答案和解析>>
科目:初中数学 来源:北京市延庆区2017-2018学年第一学期八年级期末数学试卷 题型:解答题
计算:  .
.
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2017-2018学年上学期九年级期末统一考试数学试卷 题型:解答题
如图,已知一条直线过点 ,且与抛物线
,且与抛物线 交于
交于 两点,其中点
两点,其中点 的横坐标是
的横坐标是 .
.
⑴求这条直线的函数关系式及点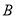 的坐标 ;
的坐标 ;
⑵在 轴上是否存在点
轴上是否存在点 ,使得△
,使得△ 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
⑶过线段 上一点
上一点 ,作
,作 ∥
∥ 轴,交抛物线于点
轴,交抛物线于点 ,点
,点 在第一象限;点
在第一象限;点 ,当点
,当点 的横坐标为何值时,
的横坐标为何值时, 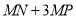 的长度最大?最大值是多少?
的长度最大?最大值是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com