
| A. | m$<\frac{1}{4}$ | B. | m$≤\frac{1}{4}$ | C. | m$≥\frac{1}{4}$ | D. | m$≤\frac{1}{4}$且m≠0 |
分析 由方程由两个实数根以及二次项系数不为0,可得出关于m的一元二次不等式组,解不等式组即可得出结论.
解答 解:由已知得:$\left\{\begin{array}{l}{{m}^{2}≠0}\\{{b}^{2}-4ac≥0}\end{array}\right.$,
即$\left\{\begin{array}{l}{{m}^{2}≠0}\\{-4m+1≥0}\end{array}\right.$,
解得:m≤$\frac{1}{4}$且m≠0.
故选D.
点评 本题考查了根的判别式,解题的关键是得出关于m的一元二次不等式组.本题属于基础题,难度不大,解决该题型题目时,根据根的个数得出关于未知数的方程(不等式或不等式组)是关键.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:填空题
 如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=$\frac{24}{5}$.
如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=$\frac{24}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC,AB=AC=2,△ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是2$\sqrt{3}$-2.
如图,在△ABC,AB=AC=2,△ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是2$\sqrt{3}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果$\frac{AD}{BC}=\frac{1}{4}$,那么$\frac{AF}{BF}$的值是( )
如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果$\frac{AD}{BC}=\frac{1}{4}$,那么$\frac{AF}{BF}$的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
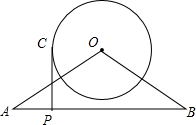 如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )
如图,在△OAB中,OA=OB=13,AB=24,以O为圆心,4为半径作⊙O,P为线段AB上动点(从A运动到B),过P作⊙O的切线PC,切点为C,则PC的取值范围是( )| A. | 3≤PC≤3$\sqrt{17}$ | B. | 5≤PC≤13 | C. | 4≤PC≤3$\sqrt{17}$ | D. | 1<PC≤13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com