
某工厂计划为学校生产A,B两种型号的学生桌椅500套,以解决1254名学生的学习问题,一套A型桌椅(一桌两椅)需木料0.5m3,一套B型桌椅(一桌三椅)需木料0.7m3,工厂现有库存木料302m3。
(1)有多少种生产方案?
(2)现要把生产的全部桌椅运往学校销售,已知每套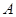 型桌椅售价150元,生产成本100元,运费2元;每套
型桌椅售价150元,生产成本100元,运费2元;每套 型桌椅售价200元,生产成本120元,运费4元,求总利润
型桌椅售价200元,生产成本120元,运费4元,求总利润 (元)与生产
(元)与生产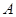 型桌椅
型桌椅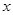 (套)之间的关系式,并确定总利润最少的方案和最少的总利润。(利润
(套)之间的关系式,并确定总利润最少的方案和最少的总利润。(利润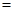 售价-生产成本-运费)
售价-生产成本-运费)
(3)按(2)的方案计算,有没有剩余木料?如果有,请直接写出用剩余木料再生产以上两种型号的桌椅,最多还可以为多少名学生提供桌椅;如果没有,请说明理由。
(1)7种;(2)生产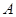 型桌椅246套、
型桌椅246套、 型桌椅254套时,总利润
型桌椅254套时,总利润 有最小值31118元;
有最小值31118元;
(3)有剩余木料 ,最多为5名学生提供桌椅.
,最多为5名学生提供桌椅.
解析试题分析:(1)设生产A型桌椅x套,则生产B型桌椅(500-x)套,由一套A型桌椅(一桌两椅)需木料0.5m3,一套B型桌椅(一桌三椅)需木料0.7m3,表示出所需的木料数,根据所需的木料数小于等于302列出不等式,再由A型一桌两椅,B型一桌三椅,计算出提供多少学生的桌椅,大于等于1254列出不等式,两不等式联立组成不等式组,求出不等式组的解集,得到x的范围,再由x为正整数即可求得结果;
(2)由利润=售价-生产成本-运费,分别表示出A型桌椅与B型桌椅每套的利润,由生产A型桌椅x套,则生产B型桌椅(500-x)套分别求出A和B的利润,相加表示出总利润y与x的一次函数关系式,由一次函数的比例系数小于0,得到此一次函数为减函数,将x的最大值代入求出对应y的值,即为最少的利润;
(3)由总利润最少时x的值,得到A型桌椅的套数,进而求出B型桌椅的套数,根据一套A型桌椅和一套B型桌椅所需的木料数,计算出用的木料数,用总木料数-用的木料数得到剩余的木料数,剩余的木料数可生产一套A型桌椅与一套B型桌椅,最多给5名学生提供桌椅.
(1)设生产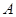 型桌椅
型桌椅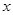 套,则生产
套,则生产 型桌椅
型桌椅 套,由题意得
套,由题意得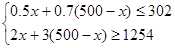
解得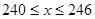
∵x为整数,
∴x的值有7个,分别为:240,241,242,243,244,245,246,
所以有7种生产方案;
(2)根据题意得:y=(150-100-2)x+(200-120-4)(500-x)=-28x+38000, 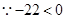 ,
, 随
随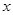 的增大而减少
的增大而减少
∴一次函数y=-28x+38000为减函数,即y随x的增大而减小, 当
当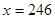 时,
时, 有最小值.
有最小值. 当生产
当生产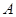 型桌椅246套、
型桌椅246套、 型桌椅254套时,总利润
型桌椅254套时,总利润 有最小值31118(元);
有最小值31118(元);
(3)当生产A型桌椅246套,B型桌椅254套时,用的木料为246×0.5+254×0.7=300.8m3,
可得剩余木料为302-300.8=1.2m3,
∵一套A型桌椅(一桌两椅)需木料0.5m3,一套B型桌椅(一桌三椅)需木料0.7m3,
则生产A型桌椅1套,B型桌椅1套时,最多为5名学生提供桌椅.
考点:一次函数的应用,一元一次不等式组的应用,方案问题
点评:此类问题难度较大,在中考中比较常见,一般在压轴题中出现,需特别注意.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
某工厂计划为学校生产A,B两种型号的学生桌椅500套,以解决1254名学生的学习问题,一套A型桌椅(一桌两椅)需木料0.5m3,一套B型桌椅(一桌三椅)需木料0.7m3,工厂现有库存木料302m3。
(1)有多少种生产方案?
(2)现要把生产的全部桌椅运往学校销售,已知每套![]() 型桌椅售价150元,生产成本100元,运费2元;每套
型桌椅售价150元,生产成本100元,运费2元;每套![]() 型桌椅售价200元,生产成本120元,运费4元,求总利润
型桌椅售价200元,生产成本120元,运费4元,求总利润![]() (元)与生产
(元)与生产![]() 型桌椅
型桌椅![]() (套)之间的关系式,并确定总利润最少的方案和最少的总利润。(利润
(套)之间的关系式,并确定总利润最少的方案和最少的总利润。(利润![]() 售价-生产成本-运费)
售价-生产成本-运费)
(3)按(2)的方案计算,有没有剩余木料?如果有,请直接写出用剩余木料再生产以上两种型号的桌椅,最多还可以为多少名学生提供桌椅;如果没有,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2012-2013学年山西九年级下学期期末考试数学试卷(解析版) 题型:解答题
某工厂计划为学校生产A,B两种型号的学生桌椅500套,以解决1254名学生的学习问题,一套A型桌椅(一桌两椅)需木料0.5m3,一套B型桌椅(一桌三椅)需木料0.7m3,工厂现有库存木料302m3。
(1)有多少种生产方案?
(2)现要把生产的全部桌椅运往学校销售,已知每套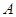 型桌椅售价150元,生产成本100元,运费2元;每套
型桌椅售价150元,生产成本100元,运费2元;每套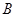 型桌椅售价200元,生产成本120元,运费4元,求总利润
型桌椅售价200元,生产成本120元,运费4元,求总利润 (元)与生产
(元)与生产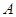 型桌椅
型桌椅 (套)之间的关系式,并确定总利润最少的方案和最少的总利润。(利润
(套)之间的关系式,并确定总利润最少的方案和最少的总利润。(利润 售价-生产成本-运费)
售价-生产成本-运费)
(3)按(2)的方案计算,有没有剩余木料?如果有,请直接写出用剩余木料再生产以上两种型号的桌椅,最多还可以为多少名学生提供桌椅;如果没有,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2012年上海市六校联考中考数学仿真测试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com