如图，直线
与y轴交于A点，与反比例函数
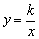（x＞0）的图象交于点M，过M作MH⊥x轴于点H，且tan∠AHO＝
.
（1）求k的值；
（2）设点N（1，a）是反比例函数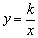
（x＞0）图像上的点，
在y轴上是否存在点P，使得PM＋PN最小，若存在，求出点P的坐标；若不存在，请说明理由.
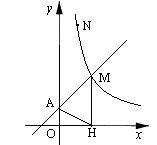
由y＝x＋1可得A（0，1），即OA＝1
∵tan∠AHO＝
，∴OH＝2
∵MH⊥x轴，∴点M的横坐标为2.
∵点M在直线y＝x＋1上，
∴点M的纵坐标为3.即M（2，3）
∵点M在
上，∴k＝2×3＝6.
（2）∵点N（1，a）在反比例函数
的图像上，
∴a＝6.即点N的坐标为（1，6）
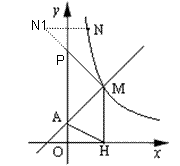
过N作N关于y轴的对称点N1，连接MN1，交y轴于P(如图)
此时PM＋PN最小.
∵N与N1关于y轴的对称，N点坐标为（1，6），
∴N1的坐标为（-1，6）
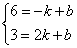设直线MN1的解析式为y＝kx＋b.
把M，N1 的坐标得
解得
∴直线MN
的解析式为
.
令x＝0，得y＝5.
∴P点坐标为（0，5）
科目：初中数学 来源： 题型：
反比例函数y＝
(k为常数,k≠0)的图象是双曲线.当k＞0时，双曲线两个分支分别在
一、三象限,在每一个象限内,y随x的增大而减小（简称增减性）；反比例函数的图象关于
原点对称（简称对称性）．
这些我们熟悉的性质，可以通过说理得到吗？
【尝试说理】
我们首先对反比例函数y＝（k＞0）的增减性来进行说理．
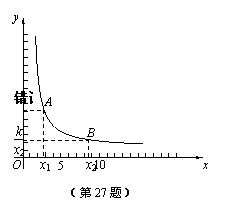
如图，当x＞0时．
在函数图象上任意取两点A、B，设A(x1，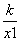
)，B(x2，
)，
且0＜x1＜ x2．
下面只需要比较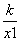和的大小．
—＝
．
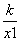∵0＜x1＜ x2，∴x1－x2＜0，x1 x2＞0，且 k＞0．
∴＜0．即
．
这说明：x1＜ x2时，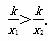
．也就是：自变量值增大了，对应的函数值反而变小了．
即：当x＞0时，y随x的增大而减小．
同理，当x＜0时，y随x的增大而减小．
（1）试说明：反比例函数y＝ （k＞0）的图象关于原点对称．
【运用推广】
（2）分别写出二次函数y＝ax2 (a＞0，a为常数)的对称性和增减性，并进行说理．
对称性： ；
增减性： ．
说理：
（3）对于二次函数y＝ax2＋bx＋c (a＞0，a，b，c为常数)，请你从增减性的角度，简要解释为何当x＝—
时函数取得最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球（除颜色外其余都相同），其中红球有2个，黑球有1个，绿球有3个，第一次任意摸出一个球（不放回），第二次再摸出一个球，则两次摸到的都是红球的概率为
A．
B．
C．
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
根据下列表格中的对应值，判断方程ax2+bx+c=0（a≠0，a，b，c为常数）的根的个数是（ ）
A．0 B．1 C．2 D．1或2
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | 0.02 | －0.01 | 0.02 | 0.04 |
查看答案和解析>>
科目：初中数学 来源： 题型：
同学们我们知道，直线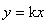
是恒过定点（0，0）的一条直线，那么你能发现直线
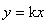+k经过的定点为 ，用类比的思想和数形结合的方法接着完成下列两题：（1）求证：无论a为何值，抛物线
.
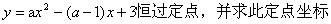（2）是否存在实数a，使二次函数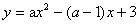
在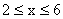
范围的最值是4？若存在，求a的范围，若不存在，请说明理由？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，AD∥BC，
，AB=AD=6，BC=9，以
为圆心在梯形内画出一个最大的扇形（图中阴影部分）的面积是 。
与反比例函数
中，x与y的对应值如下表：
>
的解为 。
（a≠0）的结果是（ ）
C. 
D. 
A． B． C． D．